הפחתת שברים ממספרים שלמים אינה קשה כפי שזה נראה. ישנן שתי דרכים עיקריות לעשות זאת: ניתן להמיר מספר שלם לשבר, או לחסוך 1 מהמספר השלם ולהפוך את 1 לשבר בעל אותו בסיס כמו השבר החסר. ברגע שיש לך שני שברים עם אותו בסיס, תוכל להתחיל להפחית. כך או כך יאפשר לך לגרוע במהירות ובקלות שברים ממספרים שלמים. אם אתה רוצה לדעת כיצד לעשות זאת, ראה שלב 1 כדי להתחיל.
שלב
שיטה 1 מתוך 2: המרת שלמים לשברים
שלב 1. רשום את הבעיה
נניח שאתה מפחית את השבר 2/7 מהמספר השלם 6. כל מה שאתה צריך לדעת הוא שהחלק העליון של השבר נקרא המונה והחלק התחתון של השבר נקרא המכנה. כתוב את השאלות הבאות: 6 - 2/7 =?
שלב 2. המר מספרים שלמים לשברים
ניתן לכתוב 6 מחדש כ- 6/1 מכיוון ש- 6/1 שווה ל -1 6 פעמים, או רק למספר 6. ניתן למקם כל מספר שלם מעל 1 והערך לא ישתנה. זה עוזר רק לשים את המספרים השלמים באותה צורה כמו השברים. עכשיו, הבעיה שלך תהיה: 6/1 - 2/7 =?
שלב 3. הכפל את המונה והמכנה של המספר השלם הראשוני במכנה של השבר הראשוני ולאחר מכן הפחת את שני השברים
עליך להפוך ל- 6/1 ו- 2/7 את אותו בסיס כדי להפחית את שני המונחים. לשם כך יהיה עליך להכפיל את המונה והמכנה 6/1 ב 7. זוהי דרך מהירה למצוא את ה- LCM, או הכפולה הקטנה ביותר, של מכני שני השברים, 1 ו- 7. 7 היא הקטנה ביותר מספר המתחלק ב- 1 ו 7. לשני השברים יש אותו מכנה, ניתן לחסר את מונה השבר על ידי השארת ערך המכנה זהה, כדי לקבל את התשובה הסופית. כך תעשה זאת:
-
ראשית, כפל 6/1 ב- 7/7:
6/1 x 7/7 = 42/7
-
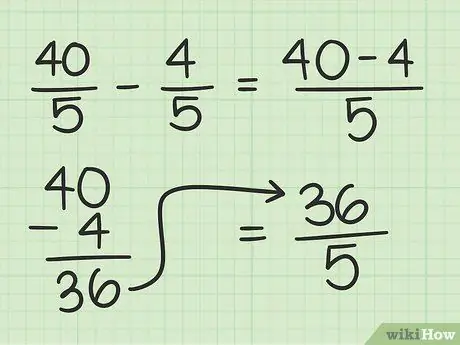
לאחר מכן, הפחת את המכנה של שני השברים:
42/7 - 2/7 = (42-2)/7 = 40/7
שלב 4. רשום את התשובה הסופית שלך
אם אתה רוצה את התשובה שלך בצורה של חלק נפוץ (כאשר המונה גדול מהמכנה), סיימת. אם אתה רוצה שהתשובה שלך תהיה מספר מעורב, שבו אתה כותב את התשובה הסופית שלך כמספר שלם אחד ושבר אחד, כל שעליך לעשות הוא לחלק את המונה במכנה, להפוך את המנה למספר שלם ולשים את השאר על המכנה הראשוני והמכנה שנותר כשבר שלך. הנה מה שאתה עושה:
- ראשית, מחלקים 40 ב- 7. 40 מחולקים ב- 7 שווים ל- 5, עם שארית 5. זה בגלל ש 7 x 5 = 35. כאשר אתה מחסר 35 מ -40, יש לך חיסור של 5, או שארית של 5.
- לאחר מכן, רשום את המספר השלם שלך: 5.
- קח את השאר, גם 5, והנח אותו מעל המכנה המקורי כדי לקבל 5/7.
- רשמו את כל המספר, ואחריו השבר החדש. אתה מקבל 5 5/7. לפיכך, השבר הנפוץ 40/7 נכתב מחדש כמספר מעורב 5 5/7.
שיטה 2 מתוך 2: הפחת 1 מהמספר הראשון
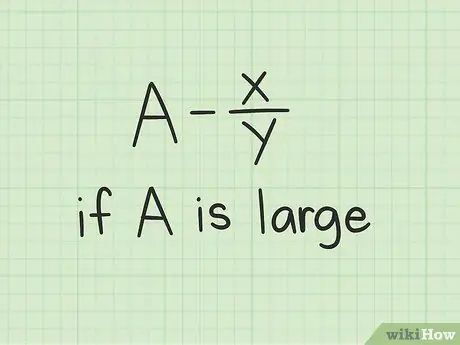
שלב 1. רשום את הבעיה
זה יהיה שימושי אם אתה יודע שאתה רוצה לכתוב את התשובה שלך כמספר מעורב. בדרך זו, יהיה לך קל יותר לקבל את התוצאה הסופית. הבה נשתמש באותה משוואה מהשיטה הראשונה, כדי לבדוק אם תוכל להשתמש בכל אחת מהשיטות בכל מצב. רשמו את השאלות הבאות:
6 - 2/7 = ?
שלב 2. הפחת את 1 מהמספר השלם
פשוט חיסרו 1 מ- 6 כדי לקבל 5. רשמו את המספר הזה.
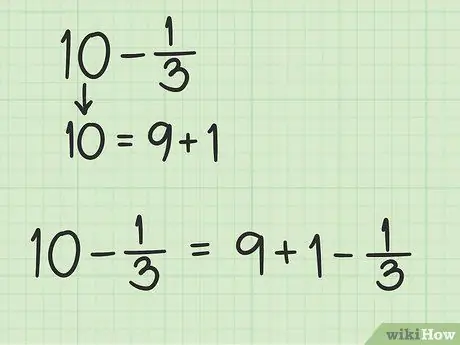
שלב 3. המר 1 לשבר בעל אותו בסיס כמו השבר
עליך להמיר 1 לשבר עם אותו מכנה כמו 7 בשעה 2/7, כך שתוכל להפחית 2/7 מהמספר. עכשיו, אתה יכול לדמיין 1 כ -1/1, ולאחר מכן לשקול את המספר שאתה צריך להכפיל במכנה ובמונה 1/1, כך שלשברים יהיה מכנה של 7 אך יהיה לו אותו ערך. ה- LCM, או הכפולה הגדולה ביותר של המכנים של 1 ו -7, היא 7, כי 7 הוא המספר הקטן ביותר שניתן לחלקו ב- 1 ו -7.
- לכן, הכפל 1/1 ב- 7/7 כדי לקבל 7/7.
- שים לב של- 7/7 יש ערך זהה ל- 1/1.
שלב 4. רשום את הבעיה החדשה שלך
כעת, הבעיה שיש לך היא 5 7/7 - 2/7. זה הופך את המספרים לקלים יותר לעבודה.
שלב 5. הפחת את השבר השני מהראשון
עכשיו, רק הפחת 2/7 מ 7/7. בעת חיסור שברים, המכנה חייב להישאר זהה, תוך חיסור המונה השני מהראשון. אז, 7/7 - 2/7 = (7-2)/7 = 5/7.
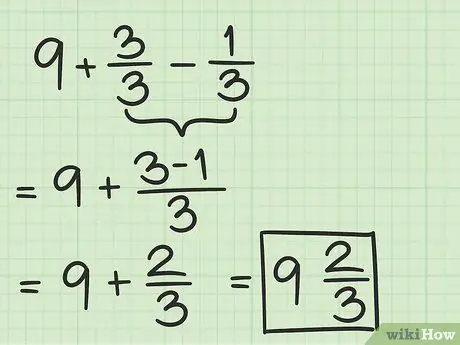
שלב 6. רשום את כל המספר עם השבר שלו כדי לקבל את התשובה הסופית שלך
כבר כתבת 5 ואתה יכול להוסיף 2/7 לידו. לפיכך, 6 - 2/7 = 5 5/7. שיטה זו קצת יותר קלה אם אתה רוצה את התשובה שלך בצורת מספר מעורב, מכיוון שאתה צריך לעבוד רק עם מספרים שלמים 1 במקום מספר שלם 6, ואינך צריך להמיר משברים נפוצים למספרים מעורבים, כפי שעשית ב- שיטה ראשונה. אתה יכול לקבוע איזו שיטה מתאימה יותר לצרכים שלך.
