ספירת שברים היא אחת מיומנויות המתמטיקה השימושיות ביותר לפיתוח. לפני ביצוע חישובי שברים, למד כיצד לזהות חלקים וסוגי שברים. לאחר מכן תוכל להוסיף או להפחית אותם. לחישובים מורכבים יותר למד כיצד להכפיל ולחלק שברים. בדרך כלל, יהיה עליך גם לפשט או להקטין שברים.
שלב
שיטה 1 מתוך 4: זיהוי שברים
שלב 1. מצא את השבר
שברים נכתבים כמספר אחד מעל הקו המפריד, ומספר אחר מתחת לקו.
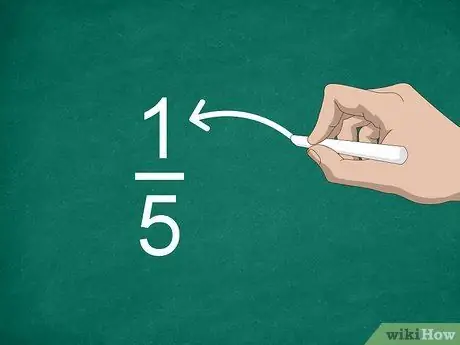
שלב 2. זהה את המונה
המספר מעל השורה נקרא מניין ומראה כמה חלקים יש בשבר.
לדוגמה, בשבר 1/5, "1" הוא המונה
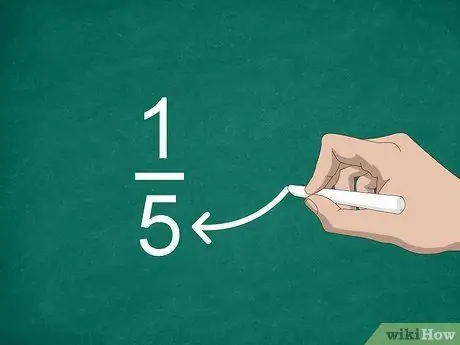
שלב 3. מצא את המכנה
המספר המוצב מתחת לקו נקרא מכנה. ערך זה מציין את מספר החלקים ש"בונים "מספר שלם.
לדוגמה, בשבר 1/5, "5" הוא המכנה ולכן ישנם חמישה חלקים לשבר
שלב 4. קבע אם השברים הם שברים סבירים או שברים לא תקינים
אם המונה קטן מהמכנה, השבר הוא שבר טבעי. בשברים לא תקינים, המונה גדול מהמכנה.
- לדוגמה, 3/4 הוא שבר סביר ו- 5/3 הוא שבר לא תקין.
- אם יש לך מספר שלם הכולל שבר, המספר ידוע כמספר מעורב. לדוגמה, 1 1/2 הוא מספר מעורב.
שיטה 2 מתוך 4: הוסף או הפחת שברים
שלב 1. זהה שברים עם אותו מכנה
אם עליך להוסיף או להפחית שברים, כל שבר חייב להיות בעל אותו מכנה לפני שתבצע את החישוב. שימו לב למכנה של כל שבר כדי לוודא שכולם שווים (דומים).
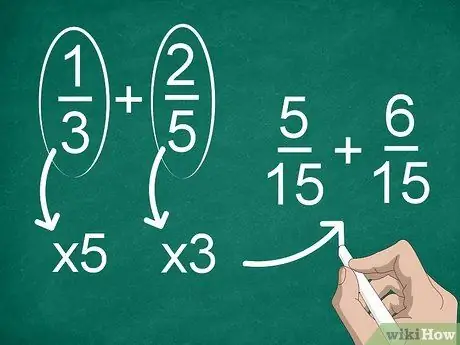
שלב 2. מצא מכנה משותף אם לכל חלק יש מכנה אחר
אם המכנים אינם זהים, יהיה עליך לשנות את השברים כדי שיהיה אותו מכנה. כדי למצוא מכנה משותף, הכפל כל שבר במכנה של האחר.
לדוגמה, כדי למצוא מכנה משותף ב- 1/3 + 2/5, הכפל את "1" ו- "3" ב- "5", ולאחר מכן הכפל את "2" ו- "5" ב- "3". כעת, יש לך את התוספת של 5/15 + 6/15. לאחר מכן תוכל לחשב את השברים
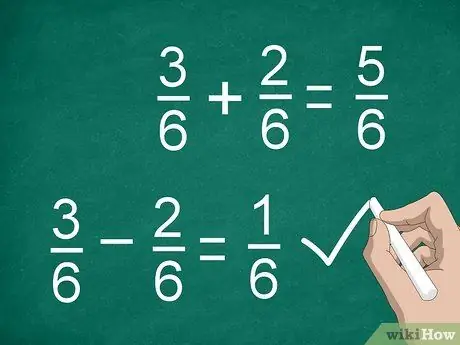
שלב 3. הוסף או הפחת את המונים כדי לחשב שברים
לאחר שמצאת מכנה משותף והכפלת את המונים (במידת הצורך), אתה מוכן להוסיף או לחסר. הוסף או הפחת את המונים והנח את התוצאה מעל לקו המפריד. כתוב את המכנה המשותף מתחת לשורה.
- לדוגמה, 3/6 - 2/6 = 1/6.
- אין להוסיף או להפחית את המכנים.
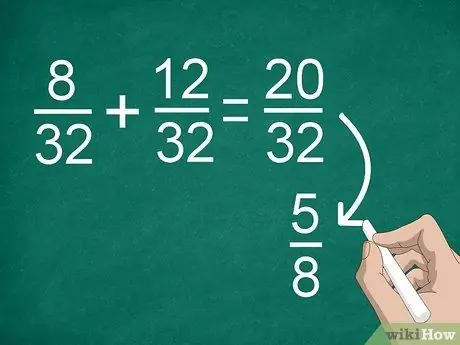
שלב 4. פשט את התוצאות במידת הצורך
אם בעבר היית צריך למצוא מכנה משותף, ייתכן שתקבל חלק גדול שתוכל לפשט. לדוגמה, אם תוסיף 8/32 +12/32, תקבל "20/32" כתוצאה מכך. ניתן לפשט את השבר הזה ל- "5/8".
שיטה 3 מתוך 4: כפל ופשט שברים
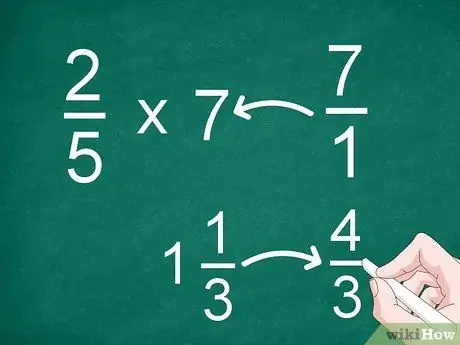
שלב 1. המרת שברים מעורבים או מספרים שלמים לשברים לא תקינים
כדי להקל על הכפל, עליך להמיר כל מספר לשבר סביר או לא תקין. אם יש לך מספרים שלמים או מספרים מעורבים שצריך להכפיל, תחילה המיר אותם לשבר נפוץ (טבעי או לא תקין).
- לדוגמה, כדי להכפיל 2/5 ב -7, המירו את "7" לשבר. לאחר מכן תוכל להכפיל 2/5 ב- 7/1.
- אם יש לך מספר מעורב כמו 1 1/3, המר אותו לשבר לא תקין ("4/3") לפני הכפלה.
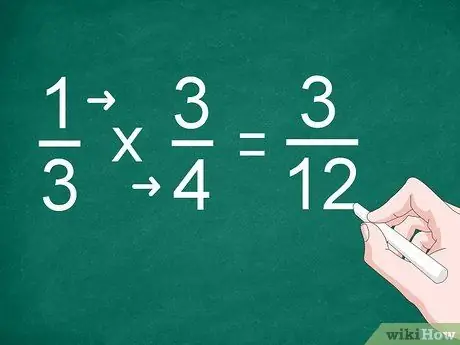
שלב 2. הכפל כל מונה ומכנה
במקום לבצע חיבור, הכפל את המונה וכתוב את התוצאה מעל לקו המפריד. עליך גם להכפיל את המכנים ולכתוב את התוצאה מתחת לשורה.
לדוגמה, כדי להכפיל 1/3 ב- 3/4, הכפל "1" ב- "3" כדי לקבל את המונה. הכפל את "3" ב- "4" כדי לקבל את המכנה. התשובה לכפל היא "3/12"
שלב 3. פשט את התוצאות
בדרך כלל, יהיה עליך לצמצם את התוצאה לצורה פשוטה יותר, במיוחד אם יש לך בהתחלה שברים לא טבעיים. מצא את הגורם המשותף הגדול ביותר והשתמש בגורם זה כדי לפשט את המונה והמכנה.
לדוגמה, עבור השבר 3/12, הגורם המשותף הגדול ביותר בין "3" לבין "12" הוא "3". חלק כל רכיב של השבר ב- "3" עד שתקבל את השבר "1/4"
שיטה 4 מתוך 4: חלקים שברים
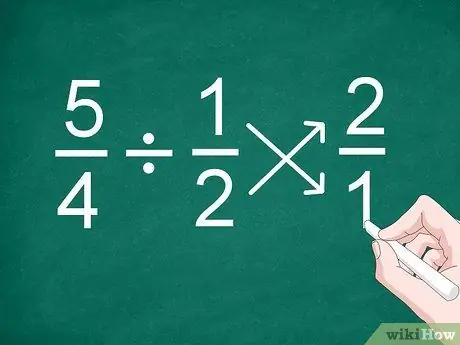
שלב 1. הפוך את המיקום של השבר השני
הדרך הקלה ביותר לחלק שברים, אפילו שברים עם מכנים שונים, היא להפוך את המיקום של השבר השני לפני חישוב התוצאה.
לדוגמה, לבעיה 5/4 1/2, הפוך את המיקום של השבר "1/2" כדי להפוך "2/1"
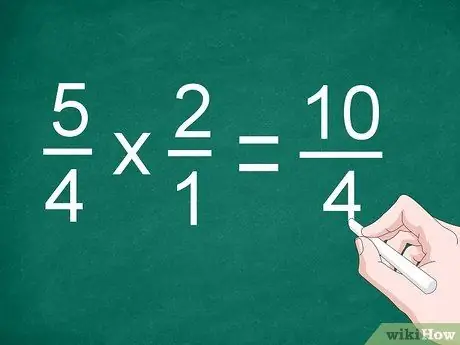
שלב 2. הכפל את המונה והמכנה
הכפל שברים ישירות כדי להכפיל את המונים. כתוב את התוצאה מעל הקו המפריד, ולאחר מכן הכפל את המכנה. רשום את התוצר של המכנים מתחת לקו.
בדוגמה הקודמת, הכפל 5/4 ב- 2/1 כדי לקבל "10/4"
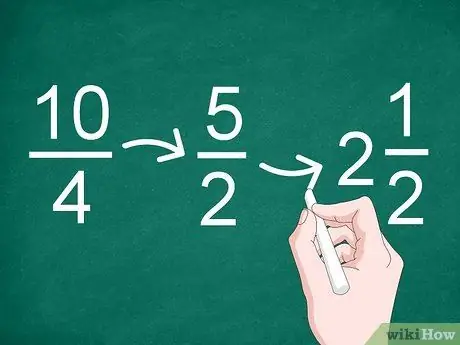
שלב 3. פשט את התוצאות במידת הצורך
אם תוצאת החלוקה היא שבר לא תקין או שניתן לצמצם אותו, פשט את השבר. השתמש בגורם המשותף הגדול ביותר כדי להפחית את השבר.
- לדוגמה, הגורם המשותף הגדול ביותר בשבר 10/4 הוא "2" ולכן תוצאת הפשט הופכת ל"5/2 "(10 מחולקת ל -2, ו -4 מחולקת ב -2).
- מכיוון שתוצאת הפשט היא שבר לא תקין, אתה יכול להמיר אותו למספר שלם ושבר (מספר מעורב). לכן ניתן לשנות את 5/2 ל- "2".
טיפים
- אם אתה עובד עם שברים מורכבים, יהיה עליך לבצע מספר צעדים נוספים כדי לפשט את השבר. עם זאת, פישוט זה עצמו הוא חלק חובה מתהליך החישוב.
- כתוב תמיד שברים בצורה מסודרת כדי להפחית את הסיכון לחישובים לא נכונים.
