עבור רוב האנשים, שברים הם החישובים המסובכים הראשונים שנתקלו בהם. מושג השברים הוא די קשה ודורש ממך ללמוד תנאים מיוחדים לשם כך. מכיוון שלשברים יש כללים מיוחדים לחיבור, חיסור, כפל וחילוק, אנשים רבים מבולבלים מכך. עם זאת, עם הרבה תרגול, כל אחד יכול ללמוד ולהשלים חישובים הקשורים לשברים.
שלב
שיטה 1 מתוך 5: הבנת שברים
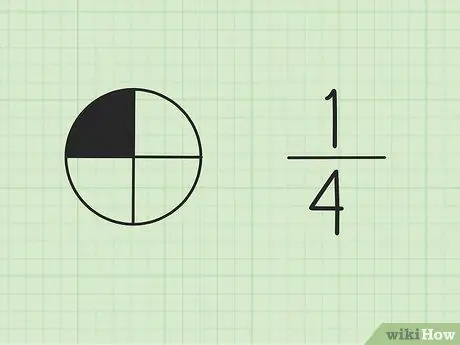
שלב 1. להבין ששברים הם חלק ממכלול
המספר בחלק העליון נקרא מניין, ומייצג את מספר חלקי הסכום. המספר בתחתית נקרא המכנה, המייצג את מספר החלקים הכולל.
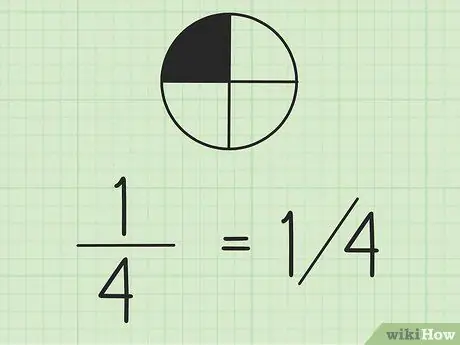
שלב 2. זכור כי אתה יכול לכתוב שברים באמצעות קווים
המספר משמאל הוא המונה והמספר מימין הוא המכנה. אם אתה עובד עם שברים על אותה שורה, כדאי לכתוב את המונה מעל המכנה.
לדוגמה, אם אתה לוקח אחת מארבע פרוסות פיצה, יש לך פיצה. אם יש לך 7/3 פיצות, זה אומר שיש לך שתי פיצות שלמות בתוספת 1 מתוך 3 פרוסות פיצה
שיטה 2 מתוך 5: ההבדל בין שברים מעורבים ופשוטים
שלב 1. להבין שמספרים מעורבים מורכבים ממספרים שלמים ושברים, למשל 2 1/3 או 45 1/2
בדרך כלל, עליך להמיר מספרים מעורבים לצורה פשוטה יותר להוספה, חיסור, הכפלה או חלוקה.
שלב 2. שנה את המספר המעורב על ידי הכפלת המספר השלם במכנה בשבר, ולאחר מכן הוספתו במונה
כתוב את התוצאה כמניין, בעוד שהמכנה אינו משתנה.
לדוגמה, כדי להמיר 2 1/3 לשבר פשוט, כפל 2 ב -3, ואז הוסף 1 וקבל 7/3
שלב 3. המרת שברים פשוטים למספרים מעורבים על ידי חלוקת המונה במכנה
כל תוצאת החלוקה נכתבת כמספר שלם, ויתר החלוקה נכתב כמניין השבר. המכנה אינו משתנה.
לדוגמה, כדי להמיר 7/3 למספר מעורב, חלק 7 ב -3 כדי לקבל 2 עם שארית 1. אז המספר המעורב הוא 2 1/3. ניתן להמיר שברים פשוטים למספרים מעורבים רק אם המונה גדול מהמכנה
שיטה 3 מתוך 5: הוספה וחיסור של שברים
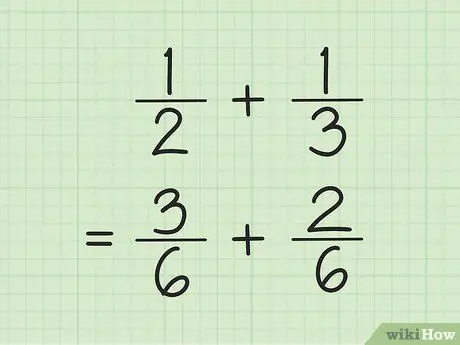
שלב 1. מצא מכנה משותף להוספת וחסר שברים
הטריק, הכפל את המספרים במכנה, ולאחר מכן הכפל כל מונה במספר המשמש לאיתור המכנה. לפעמים, אתה יכול למצוא את ה- LCM (הכפולה הפחות נפוצה) עבור המכנה על ידי הכפלת המכנים אחד בשני.
לדוגמה, כדי להוסיף ו- 1/3, תחילה מצא את ה- LCM (הכפולה הפחות נפוצה) של שני המכנים על ידי הכפלה זה מזה. לפיכך, אתה מכפיל 2 ו -3 כדי לקבל LCM 6. כפל 1 ב -3 כדי לקבל 3 כמניין החדש של השבר הראשון. הכפל 1 על 2 כדי לקבל 2 כמניין החדש של השבר השני. השברים החדשים שלך הם 3/6 ו- 2/6
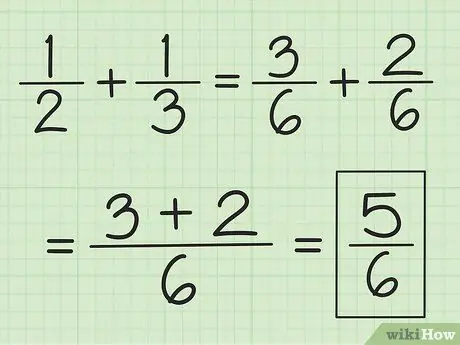
שלב 2. הוסף את שני המונים יחד ואל תשנה את המכנה
לדוגמה, 3/6 ועוד 2/6 הוא 5/6, ו 2/6 פלוס 1/6 הוא 3/6
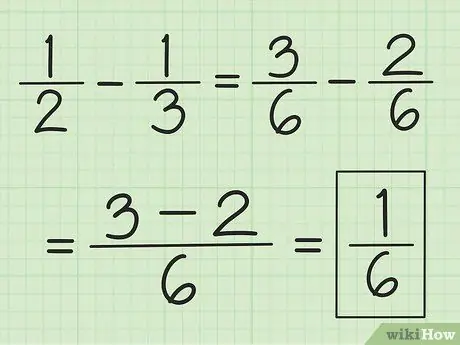
שלב 3. השתמש בטכניקה דומה לחיסור
מצאו קודם את LCM של המכנים, אך במקום להוסיף אותם, חיסרו את מספר המונה הראשון במספר השני.
לדוגמה, כדי לחסר 1/3 מ- 1/2, שנה תחילה את השברים ל- 3/6 ו- 2/6, ולאחר מכן חיסור 3 על 2 כדי לקבל 1. התוצאה היא 1/6
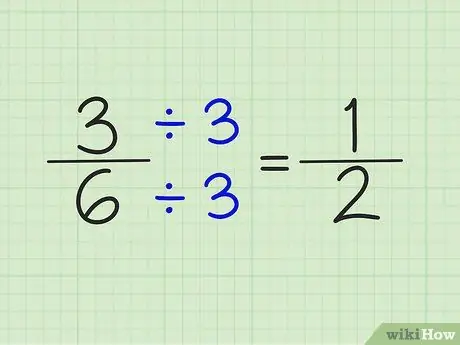
שלב 4. פשוט את השברים על ידי חלוקת המונה והמכנה באותו מספר
לדוגמה, לא ניתן לפשט את המספר 5/6. עם זאת, ניתן לפשט את 3/6 על ידי חלוקת המונה והמכנה במספר 3. התוצאה היא שבר של 1/2
שלב 5. המרת השבר למספר מעורב אם המונה גדול מהמכנה
שיטה 4 מתוך 5: הכפל וחלק שברים
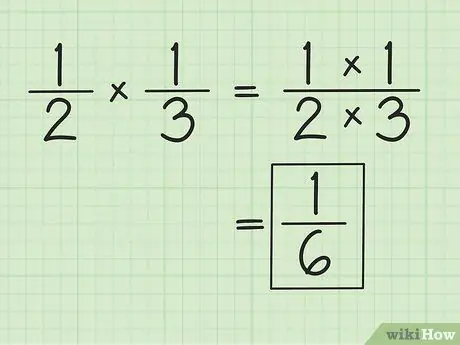
שלב 1. הכפל את המונה והמכנה בנפרד בכפל שברים
לדוגמה, כאשר מכפילים ו -1/3, התוצאה היא 1/6 (1 כפול 1 ופי 2). אינך צריך להתאים את המכנים בעת הכפלת שברים. פשט או שנה את התוצאות שהתקבלו, במידת הצורך
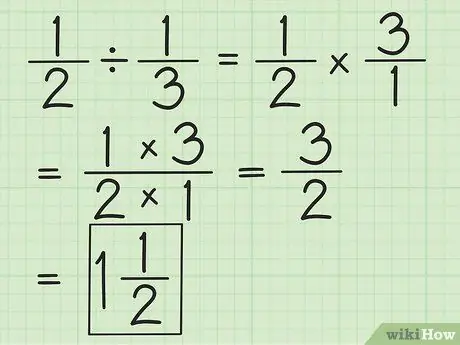
שלב 2. חלק את שני השברים על ידי היפוך השבר השני, ולאחר מכן הכפלת שניהם
לדוגמה, אם אתה רוצה לחלק 1/2 על 1/3, תחילה הפוך את השבר השני ל- 3/1. הכפל ב- 3/1 וקבל 3/2. פשט שברים או המיר למספרים מעורבים, במידת האפשר
שיטה 5 מתוך 5: עבודה עם שברים מורכבים
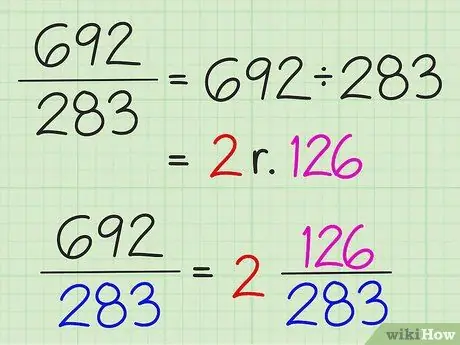
שלב 1. עבדו את כל השברים באותה צורה, גם אם נראה שהבעיה מסובכת מאוד
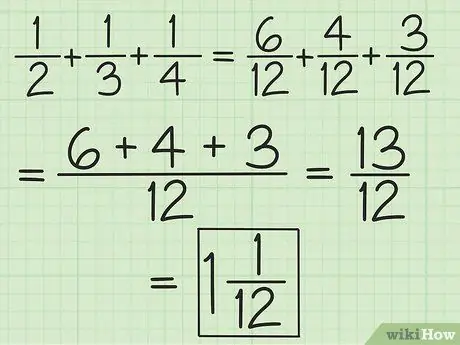
שלב 2. התאם את המכנים לכל השברים או עבודה בזוגות החל משמאל לימין כדי להוסיף ולחסור יותר משני שברים
לדוגמה, כדי להוסיף 1/2, 1/3 ו- 1/4, תוכל לשנות אותם ל- 6/12, 4/12 ו- 3/12 כדי לקבל 13/12, או להוסיף 3/6 ו -2 /6 כך שתקבל 5/6, ואז הוסף 5/6 ו- 1/4 (השווה את המכנים כך שהחלק השני יהפוך ל -3/12) כדי לקבל 13/12 (10/12 פלוס 3/12). המר אותו למספר מעורב, שהוא 1 1/12
טיפים
- זכור שלמדת לא מעט מתמטיקה. מתמטיקה היא כמו שפה שאתה יכול לבטא בשטף, ועכשיו אתה מנסה ללמוד לקרוא ולכתוב אותה.
- זכור תמיד לפשט את התוצאה הסופית של החישוב שלך, בין אם הבעיה שלך היא בצורת שבר רגיל, מספר מעורב או שבר מורכב.
