- מְחַבֵּר Jason Gerald [email protected].
- Public 2024-01-19 22:12.
- שונה לאחרונה 2025-01-23 12:18.
מתמטיקה זה קשה. קל לשכוח אפילו את מושגי היסוד כשאתה מנסה לזכור את העקרונות והשיטות השונות. להלן שתי דרכים חדשות לפשט שברים.
שלב
שיטה 1 מתוך 4: שימוש בגורם המשותף הגדול ביותר

שלב 1. רשום את גורמי המונה והמכנה
גורמים הם מספרים שאפשר להכפיל אותם כדי לקבל מספר אחר. לדוגמה, 3 ו -4 הם גורמים של 12 מכיוון שאתה יכול להכפיל אותם יחד כדי לקבל 12. כדי לרשום את הגורמים של מספר, אתה רק צריך לרשום את כל המספרים שאפשר להכפיל אותם כדי לקבל את המספר, והם מתחלקים לפי הגורמים.
-
רשום את גורמי המספר מהקטן לגדול ביותר, מבלי לשכוח לכלול את גורם 1. לדוגמה, כך אתה כותב את המונה והמכנה של השבר 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

שלב 2. מצא את הגורם המשותף הגדול ביותר (GCF) של המונה והמכנה
GCF הוא המספר הגדול ביותר שיכול לחלק באופן שווה שני מספרים או יותר. לאחר שרשמת את כל גורמי המספר, כל שעליך לעשות הוא למצוא את המספר הגדול ביותר זהה בשתי רשימות הגורמים.
-
24: 1, 2, 3, 4, 6,
שלב 8., 12, 24.
-
32: 1, 2, 4,
שלב 8., 16, 32.
-
ה- GCF של 24 ו- 32 הוא 8 מכיוון ש 8 הוא המספר הגדול ביותר שיכול לחלק באופן שווה בין 24 ו -32.

שלב 3. חלק את המונה ואת השבר על ידי ה- GCF
כעת, לאחר שקיבלת את ה- GCF, כל שעליך לעשות הוא לחלק את המונה והמכנה במספר זה כדי לפשט את השבר שלך לצורתו הפשוטה ביותר. כך תעשה זאת:
- 24/8 = 3
- 32/8 = 4
- השבר הפשוט הוא 3/4.

שלב 4. בדוק את עבודתך
אם אתה רוצה לוודא שפשטת את השבר בצורה נכונה, עליך רק להכפיל את המונה והמכנה החדש ב- GCF שלהם כדי לקבל את השבר המקורי בחזרה. כך תעשה זאת:
- 3 * 8 = 24
- 4 * 8 = 32
-
חזרת לצורתו המקורית, שהיא 24/32.
תוכל גם לבדוק את השבר כדי לוודא שלא ניתן לפשט אותו עוד יותר. מכיוון ש -3 הוא מספר ראשוני, ניתן לחלק אותו רק ב- 1 בעצמו, וארבע אינו מתחלק ב -3, כך שלא ניתן לפשט את השבר עוד יותר
שיטה 2 מתוך 4: המשך חלוקה במספרים קטנים

שלב 1. בחר מספר קטן
בשיטה זו, עליך רק לבחור מספר קטן, כגון 2, 3, 4, 5 או 7, מלכתחילה. תסתכל על השברים כדי לוודא שכל חלק מתחלק במספר שבחרת. לדוגמה, אם יש לך שבר 24/108, אל תבחר 5 מכיוון שהם אינם מתחלקים ב- 5. עם זאת, אם יש לך שבר 25/60, 5 הוא המספר הנכון לשימוש.
עבור השבר 24/32, 2 הוא מספר טוב. מכיוון ששני המספרים הם מספרים אפילו, הם מתחלקים ב -2

שלב 2. חלק את המונה ואת המכנה של השבר במספר
השבר החדש יכלול מונה ומכנה חדש, אותו תקבלו לאחר שתחלקו את החלק העליון והתחתון של השבר 24/32 ב 2. כך תעשה זאת:
- 24/2 = 12
- 32/2 = 16
- השבר החדש שלך הוא 12/16.
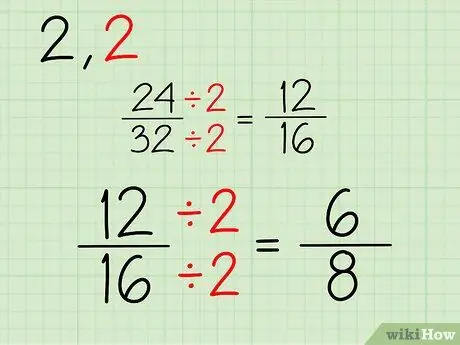
שלב 3. חזור על הפעולה
המשך בתהליך זה. מכיוון ששני המספרים הם מספרים זוגיים, תוכל להמשיך לחלק ב 2. אם אחד או שני המונים והמכנים הם מספרים אי -זוגיים, תוכל לנסות לחלק במספר אחר. להלן תהליך הפישוט של השבר 12/16:
- 12/2 = 6
- 16/2 = 8
- השבר החדש שלך הוא 6/8.

שלב 4. המשך לחלק את המספר עד שהוא כבר אינו מתחלק
המונה והמכנה החדשים הם גם מספרים אחידים, כך שתוכל להמשיך לחלק ב 2. הנה איך לעשות זאת:
- 6/2 = 3
- 8/2 = 4
- השבר החדש שלך הוא 3/4.

שלב 5. ודא שלא ניתן לפשט את השבר
בשבר 3/4, 3 הוא מספר ראשוני, כך שהגורמים הם רק 1 והוא עצמו, ו -4 אינו מתחלק ב -3, כך שלא ניתן לפשט את השבר עוד יותר. אם כבר אי אפשר לחלק את המונה או המכנה של השבר במספר שבחרת, עדיין תוכל לחלק אותו במספר אחר.
לדוגמה, אם יש לך את השבר 10/40 ואתה מחלק את המונה והמכנה ב -5, התוצאה היא 2/8. אתה לא יכול להמשיך לחלק את המונה והשבר ב- 5, אבל אתה יכול לחלק את שניהם ב -2 כך שהתוצאה הסופית היא 1/4

שלב 6. בדוק את עבודתך
הכפל 3/4 על 2/2 שוב שלוש פעמים, כדי לוודא שאתה מקבל את השבר הראשוני, שהוא 24/32. כך תעשה זאת:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- שימו לב שאתם מחלקים 24/32 ב- 2 * 2 * 2, שזהה לחלוקה ב- 8, ה- GCF הגדול ביותר של 24 ו -32.
שיטה 3 מתוך 4: כתיבת הגורמים

שלב 1. רשום את השבר שלך
השאר רווח גדול בצד ימין של הנייר שלך - תצטרך אותו כדי לרשום את הגורמים.

שלב 2. רשום את גורמי המונה והמכנה
לבד הגורמים של השניים. הדרך הקלה ביותר היא שהגורמים ייכתבו זה על זה. התחל עם המספר 1 ורשום את הגורמים.
-
לדוגמה, אם השבר שלך הוא 24/60, התחל עם 24.
רשמו: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
ואז, המספר 60.
רשמו: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

שלב 3. מצא וחלק לפי הגורם המשותף הגדול ביותר
ניתן לכתוב מונח זה כ- GCF בספר המודפס שלך. מהו המספר הגדול ביותר שיכול לחלק את המונה והמכנה? לא משנה מה המספר, חלק את שני המספרים במספר זה.
לדוגמא שלנו, המספר הגדול ביותר שהוא גורם לשני המספרים הוא 12. לפיכך, אנו מחלקים 24 על 12 ו -60 על 12, נותנים לנו 2/5 - השבר הפשוט שלנו
שיטה 4 מתוך 4: שימוש בעץ פקטור

שלב 1. מצא את הגורמים העיקריים של המונה והמכנה
מספר ראשוני הוא מספר שלא ניתן לחלק אותו במספר אחר (מלבד עצמו ו -1, כמובן). 2, 3, 5, 7 ו -11 הן דוגמאות למספרים ראשוניים.
- התחל עם המונה. מ -24, מתחלקים ל -2 ו -12. מכיוון ש -2 הוא כבר מספר ראשוני, אתה כבר לא צריך לחלק אותו! לאחר מכן שוברים 12 ל -2 מספרים: 2 ו- 6. 2 הם מספרים ראשוניים - נהדר! כעת חלק את 6 ל -2 מספרים: 2 ו- 3. כעת יש לך 2, 2, 2 ו -3 כמספרים ראשוניים שלך.
- עכשיו תעבוד על המכנה. החל מ -60, חלק את העץ שלך ל -2 ו -30. 30 לאחר מכן חלק ל- 2 ו- 15. לאחר מכן חלק 15 ל -3 ו -5, שניהם מספרים ראשוניים. עכשיו יש לך 2, 2, 3 ו -5 כמספרים ראשוניים שלך.
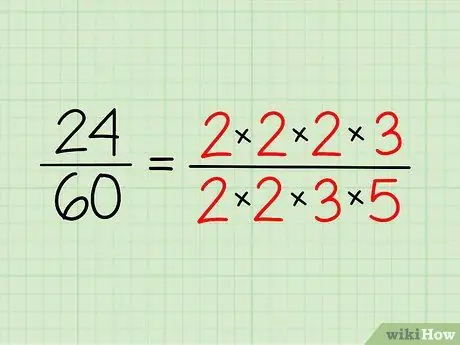
שלב 2. רשום את הגורם העיקרי של כל מספר
רשום את המספרים הראשוניים שיש לך לכל מספר וכתוב אותם בצורה של כפל. אתה לא צריך להכפיל את זה - זו רק דרך להקל על הצפייה.
- אז, עבור 24, יש לך 2 x 2 x 2 x 3 = 24.
- עבור 60, יש לך 2 x 2 x 3 x 5 = 60

שלב 3. סלק את אותם גורמים
ניתן למחוק כל מספר שהוא חלק משני המספרים. בדוגמה זו, הגורמים השווים הם זוג 2s ואחד 3. להתראות!
- השאר 2 ו -5 - או 2/5! אותה תשובה קיבלנו את הדרך למעלה.
- אם המונה והמכנה של השבר הם מספרים שווים, אל תחלק רק בשניים. המשך לבצע את החלוקה עד שלא ניתן לחלק את המספר שתקבל שוב.






