ניתן למצוא קווים בכל מקום במתמטיקה, בין אם אתה לוקח אלגברה 1, גיאומטריה או אלגברה 2. אם אתה יודע כיצד למצוא את שיפוע הקו, הרבה דברים יתבררו, למשל אם שני הקווים מקבילים או בניצב., מצטלבים ומושגים רבים אחרים. מציאת שיפוע של קו היא למעשה קלה מאוד. המשך לקרוא כמה צעדים פשוטים שבהם תוכל ללמוד כיצד למצוא שיפועי קו.
שלב
שיטה 1 מתוך 2: נוסחת Gradient
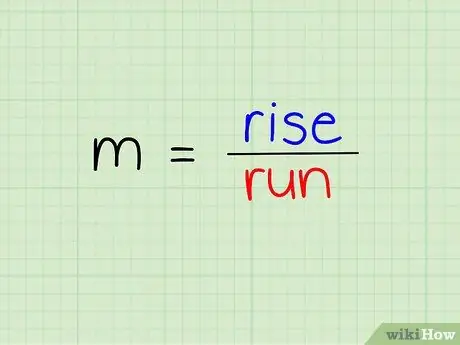
שלב 1. הבנת נוסחת השיפוע
שיפוע מוגדר כאנכי חלקי אופקי.
שיטה 2 מתוך 2: מציאת השיפוע
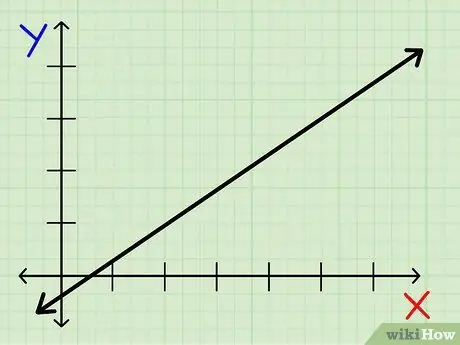
שלב 1. מצא את הקו שאליו ברצונך למצוא את שיפוע
וודא שהקו ישר. אינך יכול למצוא את שיפוע של קו שאינו ישר.
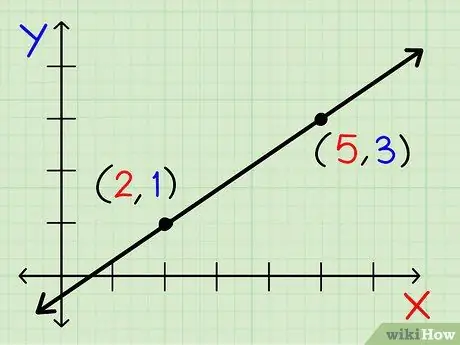
שלב 2. בחר כל שני קואורדינטות שהקו עובר
הקואורדינטות הן נקודות x ו- y הכתובות (x, y). לא משנה באיזו נקודה תבחר, כל עוד הנקודות שונות ושוכבות על אותו קו.
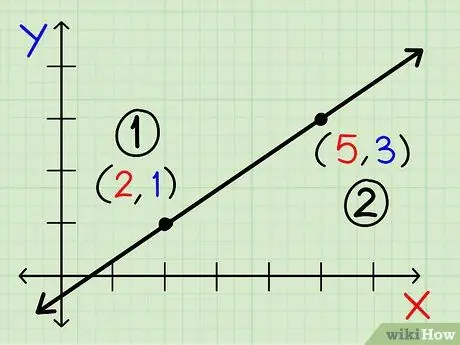
שלב 3. בחר את נקודת הקואורדינטות הדומיננטיות במשוואה שלך
זה לא משנה באיזו נקודה תבחר, כל עוד הערך תמיד זהה במהלך החישוב. הקואורדינטה הדומיננטית היא x 1 ו- y 1. הקואורדינטות האחרות הן x 2 ו- y 2.
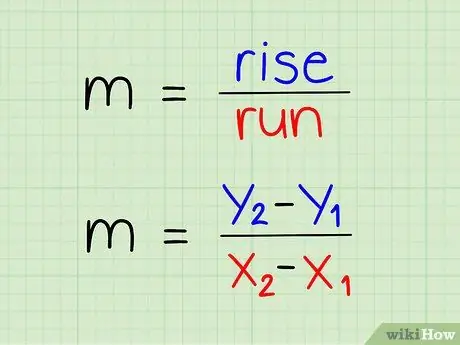
שלב 4. כתוב את המשוואה שלך עם קואורדינטת y למעלה וקואורדינטת x למטה
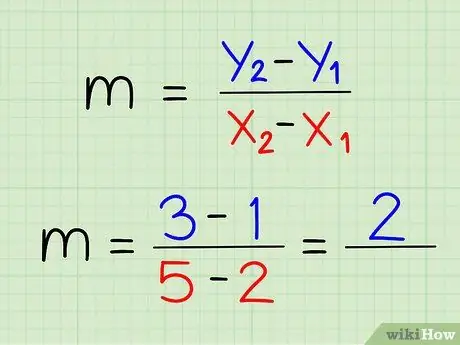
שלב 5. הפחת את שני קואורדינטות ה- y זה מזה
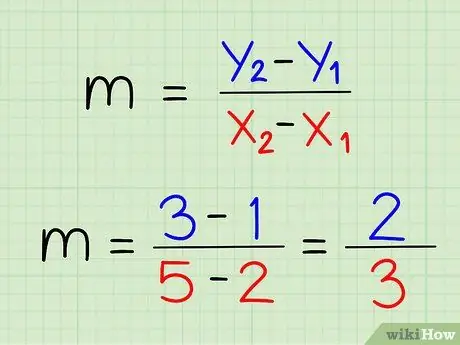
שלב 6. הפחת את שני הקואורדינטות x זה מזה
שלב 7. חלק את התוצאה של הפחתת קואורדינטות ה- y לפי התוצאה של חיסור קואורדינטת ה- x
פשט את המספר אם ניתן לפשט אותו.
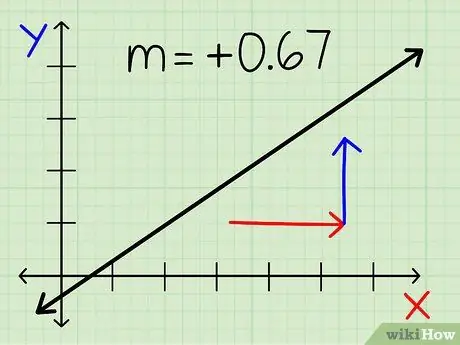
שלב 8. בדוק שוב אם התשובה שלך הגיונית
- קו העובר משמאל לימין הוא תמיד חיובי, גם אם הוא שבר.
- הקו שיורד משמאל לימין הוא תמיד שלילי, גם אם זה שבר.
דוגמא
- ידוע: קו AB.
- קואורדינטות: A - (-2, 0) B - (0, -2)
- (י2-י1): -2-0 = -2; אנכי = -2
- (איקס2-איקס1): 0-(-2) = 2; אופקי = 2
-
שיפוע של קו AB = (אנכי/אופקי) = -1.
טיפים
- אם כבר בחרת את הקואורדינטות של הנקודה הדומיננטית שלך, אל תחליף אותן לקואורדינטות אחרות או שהתשובה שלך תהיה שגויה.
- תוכלו למצוא m בנוסחת הקווים, שהיא: y = mx+b, כאשר y הוא קואורדינטת y של כל נקודה, m הוא שיפוע, x הוא קואורדינטת x המתאימה לקואורדינטת y של כל נקודה, ו- b הוא יירוט ה- y.
- תוכל גם לחפש בספר הלימוד של בית הספר שלך או לשאול את המורה שלך.
