- מְחַבֵּר Jason Gerald [email protected].
- Public 2024-01-19 22:12.
- שונה לאחרונה 2025-01-23 12:18.
חיסור הוא פשוט חיסור מספר אחד לאחר. קל לחסר מספר שלם אחד לאחר, אך חיסור יכול להיות מסובך אם אתה מפחית שברים או עשרוניים. לאחר שתבין חיסור, תוכל להשתמש במושגי מתמטיקה מורכבים יותר, ותוכל להוסיף, להכפיל ולחלק מספרים ביתר קלות.
שלב
שיטה 1 מתוך 6: הפחתת מספרים גדולים על ידי הלוואות

שלב 1. רשום מספר גדול
לדוגמה, אתה רוצה לפתור 32 - 17. כתוב קודם כל 32.

שלב 2. כתוב את המספר הקטן ממש מתחתיו
וודא שאתה ממקם את ערכי העשר ואחד בעמודות הנכונות, כך ש -3 מתוך 32 יהיה ישירות מעל 1 מתוך 17 ו- 2 מתוך 32 יהיה ישירות מעל 7 מתוך 17.
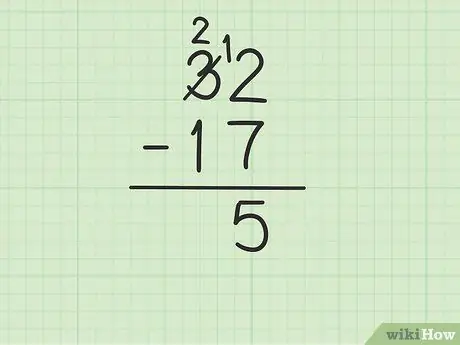
שלב 3. הפחת את המספר העליון בעמודה יחידות מהמספר בתחתית
עם זאת, זה יכול להסתבך אם המספר התחתון גדול מהמספר העליון. במקרה זה, 7 גדול מ- 2. הנה מה שאתה צריך לעשות:
- עליך להשאיל מהמספר 3 מתוך 32 (הידוע גם בשם קיבוץ), כדי להפוך 2 ל -12.
- חצו את המספר 3 מתוך 32 והחליפו אותו במספר 2, בעוד המספר 2 הופך ל -12.
- עכשיו אתה יכול להפחית 12 - 7, שזה שווה 5. כתוב 5 מתחת לשני המספרים שאתה מפחית כך שהם יהיו בעמודה היחידות של השורה החדשה.
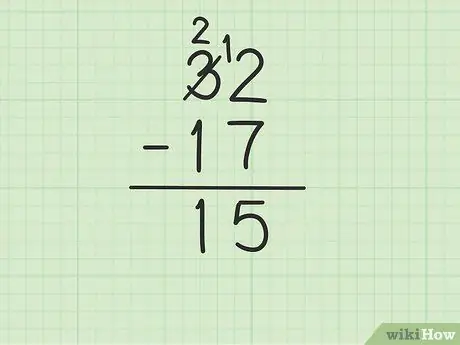
שלב 4. הפחת את המספר העליון בעמודה עשרות מהמספר התחתון
זכור 3 הפך 2. הפחת כעת 1 מ -17 מ -2 מלעיל כדי לקבל (2-1) 1. כתוב 1 למטה, בעמודה עשרות, משמאל ל -5 בעמודה יחידות. אתה כותב 15. כלומר 32 - 17 = 15.
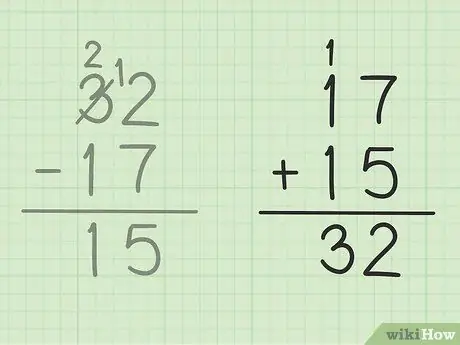
שלב 5. בדוק את עבודתך
אם אתה רוצה לוודא שחיסרת שני מספרים בצורה נכונה, כל שעליך לעשות הוא להוסיף את התשובה שלך למספר הקטן יותר כדי ליצור מספר גדול. בבעיה זו, עליך להוסיף את התשובה שלך, 15 למספר החיסור הקטן יותר, 17. 15 + 17 = 32, כך שהתשובה שלך תהיה נכונה. בטוח!
שיטה 2 מתוך 6: הפחת מספרים קטנים
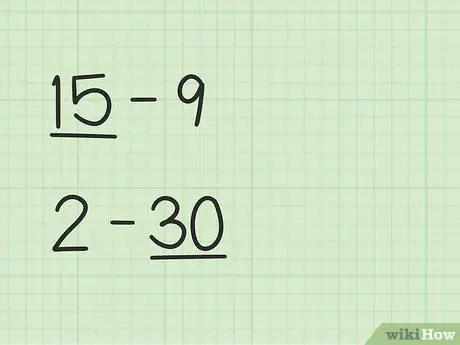
שלב 1. מצא את המספר הגדול יותר
לבעיות כמו 15 -9 תהיה דרך שונה מ -2 -30.
- בשאלות 15 - 9 המספר הראשון, 15, גדול מהמספר השני, 9.
- בשאלות 2 - 30 המספר השני, 30, גדול מהמספר הראשון, 2.
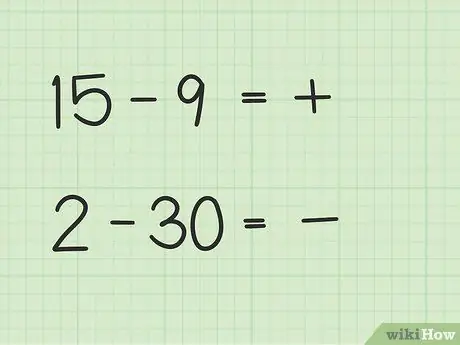
שלב 2. החליטו אם התשובה שלכם תהיה חיובית או שלילית
אם המספר הראשון גדול יותר, התשובה חיובית. אם המספר השני גדול יותר, התשובה שלילית.
- בשאלה הראשונה, 15 - 9, התשובה שלך חיובית מכיוון שהמספר הראשון גדול מהמספר השני.
- בשאלה השנייה, 2 - 30, התשובה שלך שלילית מכיוון שהמספר השני גדול מהמספר הראשון.
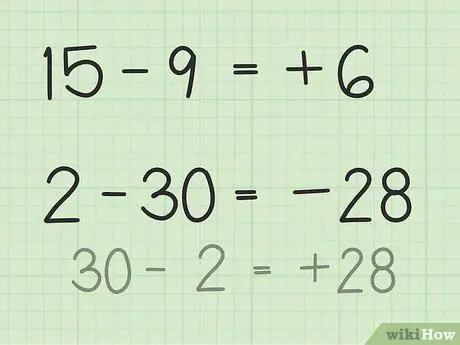
שלב 3. מצא את ההבדל בין שני מספרים
כדי להפחית שני מספרים, עליך לדמיין את ההבדל בין שני המספרים ולחשב את המספרים ביניהם.
- לשאלות 15 - 9, דמיין ערימה של 15 שבבי פוקר. זרק 9 שבבים ורק 6. אז, 15 - 9 = 6. אתה יכול גם לדמיין שורת מספרים. תחשוב על המספרים מ -1 עד 15, ואז זרוק או החזר 9 יחידות כך שתקבל 6.
- לשאלות 2 - 30 הדרך הקלה ביותר לפתור זאת היא להפוך את המספר ולהפוך את התוצאה לשלילית לאחר חיסור. אז, 30 - 2 = 28 כך של 28 ו- 30 יש הבדל של 2. כעת, הפוך את התוצאה לשלילית מכיוון שכבר קבעת שהתשובה שלילית מכיוון שהמספר השני גדול מהמספר הראשון. אז, 2 -30 = -28.
שיטה 3 מתוך 6: הפחתת עשרוניות
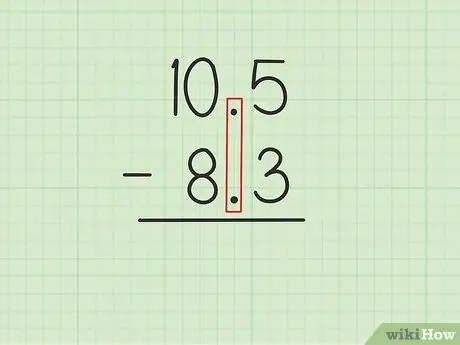
שלב 1. כתוב את המספר הגדול על המספר הקטן יותר כאשר הנקודות העשרוניות מיושרות
נניח שאתה רוצה לפתור את הבעיות הבאות: 10, 5 - 8, 3. כתוב 10, 5 על 8, 3 כך שהנקודות העשרוניות של שני המספרים יהיו מקבילות., 5 מתוך 10, 5 חייבים להיות ישירות מעל, 3 מתוך 8, 3 ו -0 מתוך 10, 5 חייבים להיות מעל 8 מתוך 8, 3.
אם יש לך בעיה מכיוון שלשני המספרים אין אותו מספר אחרי הנקודה העשרונית, כתוב 0 בריק עד לסכום המספרים זהה. לדוגמה, הבעיה היא 5, 32 - 4, 2, אתה יכול לכתוב אותה כ -5, 32 - 4, 2 0. זה לא ישנה את ערך המספר השני, אך יקל על חיסור שני המספרים.

שלב 2. הפחת את המספר העליון בעמודה עשרות מהמספר שלהלן
במקרה זה, עליך להפחית 3 מ -5. 5 - 3 = 2, לכן עליך לכתוב 2 תחת 3 מתוך 8, 3.
הקפד לשים נקודה עשרונית בתשובה, כך שתיכתב, 2

שלב 3. הפחת את המספר שמעל העמודה יחידות מהמספר שמתחתיו
אתה צריך להפחית 8 מ- 0. לווה 1 מחלק העשרות כדי לשנות 0 ל -10 ולחסור 10 - 8 כדי לקבל 2. אתה יכול גם לספור 10 - 8 בלי ללוות כי אין מספרים בעמודת העשרות השנייה. כתוב את התשובה תחת 8, משמאל לנקודה העשרונית.

שלב 4. רשום את התוצאה הסופית שלך
התוצאה הסופית שלך היא 2, 2.

שלב 5. בדוק את עבודתך
אם אתה רוצה לוודא שהחיסור העשרוני שלך נכון, כל שעליך לעשות הוא להוסיף את התשובה שלך למספר הקטן יותר כדי להפוך את המספר הגדול יותר. 2, 2 + 8, 3 = 10, 5, אז סיימת.
שיטה 4 מתוך 6: הפחת שברים

שלב 1. יישר את המכנה ואת מונה השבר
נניח שאתה רוצה לפתור בעיות 13/10 - 3/5. כתוב את הבעיה כך ששני המונים, 13 ו -3 ושני המכנים, 10 ו -5 נמצאים זה בזה. שני מספרים אלה מופרדים בסימן חיסור. זה יעזור לך לדמיין את הבעיה ולפתור אותה ביתר קלות.

שלב 2. מצא את המכנה הכי פחות משותף
המכנה הכי פחות משותף הוא המספר הקטן ביותר שניתן לחלק בשני מספרים. בדוגמה זו, עליך למצוא את המכנה המשותף הקטן ביותר שניתן לחלק ב- 10 ו- 5. תמצא כי 10 הוא המכנה המשותף הקטן ביותר לשני המספרים מכיוון ש -10 מתחלק ב- 10 ו- 5.
שים לב שהמכנה הפחות משותף של שני מספרים הוא לא תמיד אחד מהם. לדוגמה, המכנה המשותף הקטן ביותר עבור 3 ו -2 הוא 6 מכיוון ש 6 הוא המספר הקטן ביותר שניתן לחלק בשני מספרים
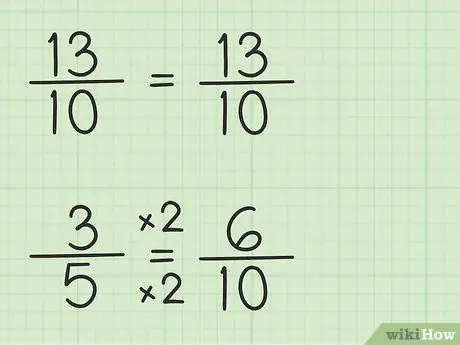
שלב 3. רשום את השברים באמצעות אותו מכנה
ניתן לכתוב את השבר 13/10 באותו אופן מכיוון שהמכנה הוא 10, המכנה המשותף הקטן ביותר, שהוא 10, כפול 1. עם זאת, יש לשכתב את השבר 3/5 מכיוון שהמכנה הוא 5, המכנה המשותף הקטן ביותר, שזה 10, כפול 2. לכן יש להכפיל את השבר 3/5 ב 2/2 כדי להפוך את המכנה 10, כך ש 3/5 x 2/2 = 6/10. מצאת את החלק השווה. 3/5 שווה ל 6/10 אם כי 6/10 מאפשר לך לגרוע מהמספר הראשון, 13/10.
כתוב שאלה חדשה כמו זו: 13/10 - 6/10
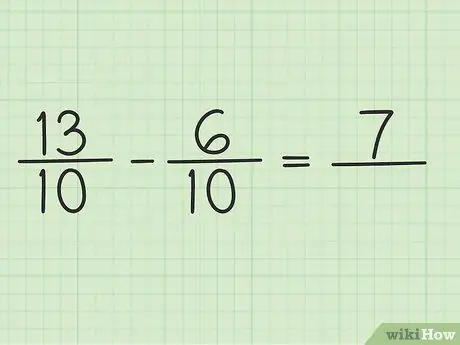
שלב 4. הפחת את המונה לשני מספרים
פשוט חיסרו 13 - 6 כך שהתוצאה תהיה 7. לא ניתן לשנות את המכנה של השבר.
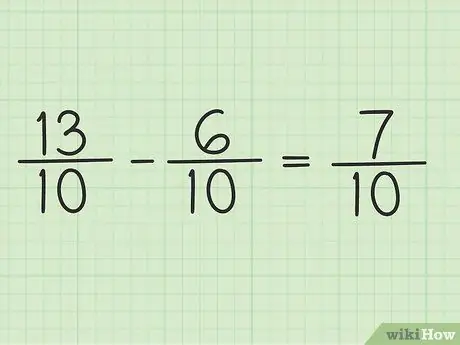
שלב 5. כתוב את המונה החדש על אותו מכנה כדי לקבל את התוצאה הסופית
המונה החדש הוא 7. לשני השברים יש מכנה של 10. התוצאה הסופית שלך היא 7/10.
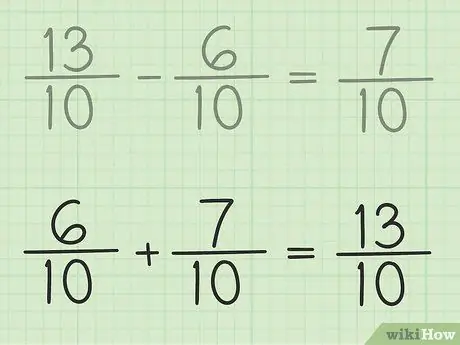
שלב 6. בדוק את עבודתך
אם אתה רוצה לוודא שאתה מפחית את השבר בצורה נכונה, פשוט צבר את התשובה שלך ואת השבר הקטן יותר כך שהתוצאה תהיה חלק גדול יותר. 7/10 + 6/10 = 13/10. זה גמור.
שיטה 5 מתוך 6: הפחתת שברים ממספרים שלמים

שלב 1. רשום את הבעיה
לדוגמה, נניח שאתה רוצה לפתור את הבעיה הבאה: 5 -. תרשום את זה.
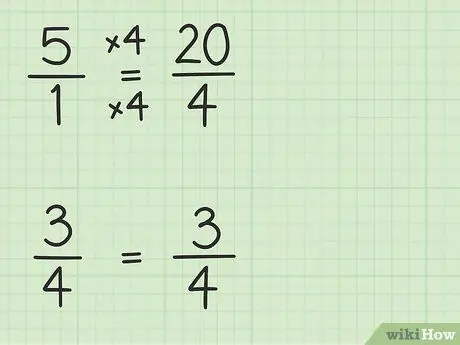
שלב 2. המר מספרים שלמים לשברים בעלי אותו מכנה כמו שברים אחרים
אתה תמיר 5 לשבר עם מכנה 4 כדי להיות מסוגל לחסר שני מספרים. אז אתה צריך לחשוב על 5 כשבריר של 5/1. לאחר מכן, תוכל להכפיל את המונה ואת המכנה של השבר החדש ב -4 כדי להפוך את המכנים של שני המספרים זהים. אז 5/1 x 4/4 = 20/4. חלק זה שווה ל -5, אך מאפשר לך לחסר שני מספרים.
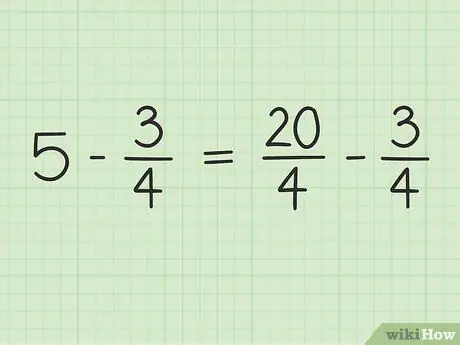
שלב 3. כתוב מחדש את הבעיה
ניתן לכתוב את הבעיה החדשה כך: 20/4 - 3/4.
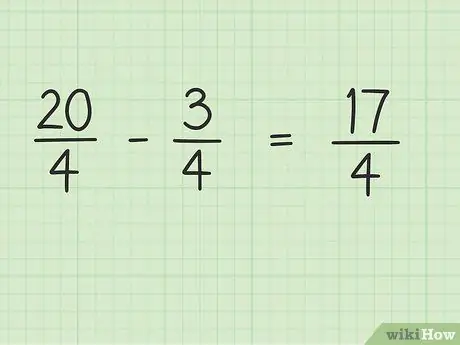
שלב 4. הפחת את מונה השבר, בעוד שהמכנה נשאר זהה
כעת, רק הפחת 20 עד 3 כדי לקבל את התוצאה הסופית. 20 - 3 = 17, אז 17 הוא המונה החדש. אתה יכול להשאיר את המכנה אותו דבר.
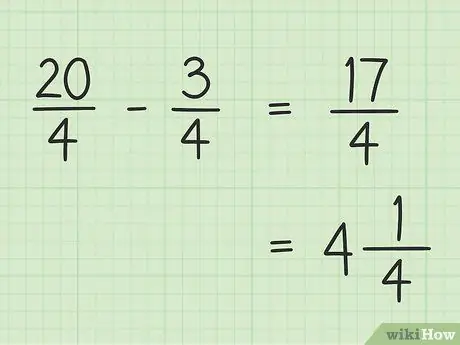
שלב 5. רשום את התוצאה הסופית שלך
התוצאה הסופית שלך היא 17/4. אם אתה רוצה לכתוב אותו כמספר מעורב, חלק 17 ב -4 כך שהתוצאה תהיה 4 והשאר 1, כך ש- 17/4 הסופי שלך יהיה 4.
שיטה 6 מתוך 6: הפחתת משתנים
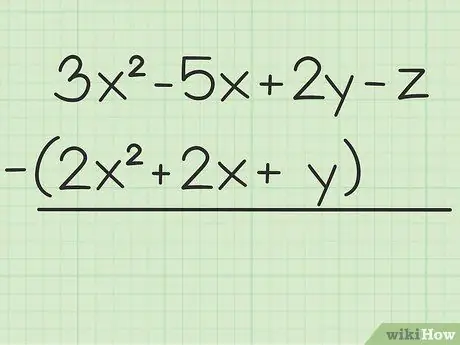
שלב 1. רשום את הבעיה שברצונך לפתור
למשל השאלה הבאה: 3x2 - 5x + 2y - z - (2x2 + 2x + y). כתוב את קבוצת המשתנים הראשונה על השנייה.
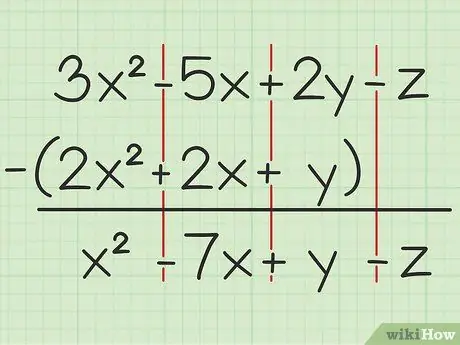
שלב 2. הפחת את אותם המשתנים
אם אתה נתקל במשתנה, תוכל להוסיף או להפחית את אותו משתנה ואשר כתוב באותה מידה בריבוע. זה אומר שאתה יכול להפחית 4x2 מ 7x2, אבל לא יכול להפחית 4x מ -4y. אז אתה יכול לפרק את הבעיה כך:
- 3x2 - 2x2 = x2
- -5x -2x = -7x
- 2y - y = y
- -z -0 = -z
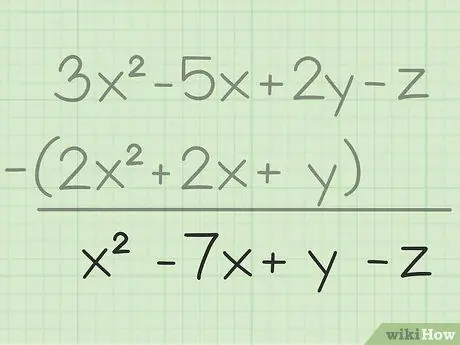
שלב 3. רשום את התוצאה הסופית שלך
הפחתת את כל אותם המשתנים, כל שעליך לעשות הוא לכתוב את התוצאה הסופית שתכיל את כל המשתנים שחיסרת. להלן התוצאה הסופית:






