כיצד לחשב מהירות ממוצעת: 12 שלבים (עם תמונות)

2024 מְחַבֵּר: Jason Gerald | [email protected]. שונה לאחרונה: 2024-02-01 14:13

כל מה שאתה צריך כדי לחשב את המהירות הממוצעת הוא התזוזה הכוללת. או שינוי המיקום, והזמן הכולל. זכור כי מהירות מחשבת גם את הכיוון והמהירות של אובייקט, לכן כלול כיוון בתשובתך, כגון "צפון", "קדמי" או "שמאל". אם בעיית חישוב המהירות שלך כוללת גם האצה מתמדת, תוכל ללמוד דרך מהירה למצוא את התשובה אפילו קלה יותר.

שלב

שיטה 1 מתוך 2: חישוב המהירות הממוצעת של התזוזה והזמן

שלב 1. זכור שמהירות כוללת את המהירות והכיוון של אובייקט

מהירות מתארת את הקצב שבו משתנה מיקום האובייקט. זה קשור לא רק למהירות הנעת האובייקט, אלא גם לכיוון שלו. "100 מטר לשנייה דרומה" הוא ערך מהירות שונה מאשר "100 מטר לשנייה מזרחה".

• כמויות בעלות כיוון נקראות כמויות וקטוריות '. ניתן להבחין בין כמות זו מכמות נטולת כיוון הנקראת כמות סקלרית על ידי כתיבת חץ מעל המשתנה. לדוגמה, הסימון v מייצג את השיעור, בעוד הסימון v ^→ מייצג מהירות או מהירות + כיוון. סימון v המשמש במאמר זה מייצג מהירות.
• בבעיות מדעיות, עליך להשתמש במטרים או ביחידות מטריות אחרות כדי להביע מרחק, בעוד למטרות יומיומיות אתה יכול להשתמש בכל יחידה שאתה אוהב.

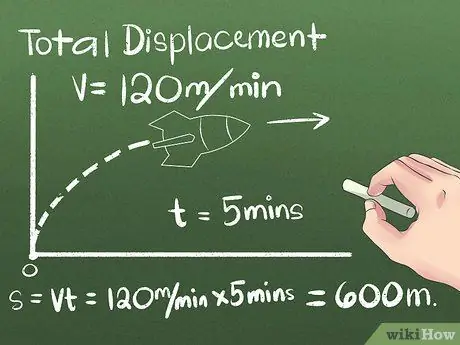
שלב 2. מצא את ערך העקירה הכולל

עקירה היא השינוי במיקום האובייקט, או המרחק והכיוון בין נקודות ההתחלה והסיום שלו. ניתן להזניח את הכיוון שהאובייקט נע לפני שהוא מגיע למיקומו הסופי, מכיוון שלוקחים בחשבון רק את המרחק בין נקודות ההתחלה והסיום. בדוגמה הראשונה נשתמש באובייקט הנע במהירות קבועה בכיוון אחד:

• נניח שרקטה נעה צפונה למשך 5 דקות במהירות קבועה של 120 מטרים לדקה. כדי לחשב את המיקום הסופי, השתמש בנוסחה s = vt, או השתמש בחשיבה מעשית לחישוב המרחק שעברה הרקטה לאחר מכן (5 דקות) (120 מטר/דקה) = 600 מטר צפונה מנקודת ההתחלה.
• לבעיות הכרוכות בתאוצה קבועה, תוכל לפתור אותן באמצעות s = vt + at², או השתמש בשיטה הקצרה המתוארת בסעיף אחר כדי למצוא את התשובה.

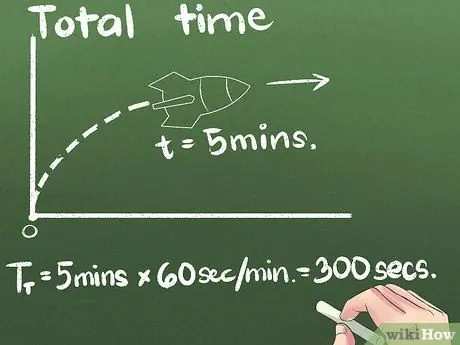
שלב 3. מצא את כל הזמן המושקע

בדוגמה שלנו, הרקטה נעה קדימה למשך 5 דקות. אתה יכול לבטא את המהירות הממוצעת בכל יחידת זמן, אך השנייה היא יחידת התקן המדעי הבינלאומי. נשנה את יחידות השניות בדוגמה זו: (5 דקות) x (60 שניות/דקה) = 300 שניות.

אפילו בבעיות מדעיות, אם השאלה משתמשת בשעה או ביחידת זמן גדולה יותר, יהיה קל יותר לחשב את המהירות תחילה, ולאחר מכן להמיר את התשובה הסופית למטר/שנייה

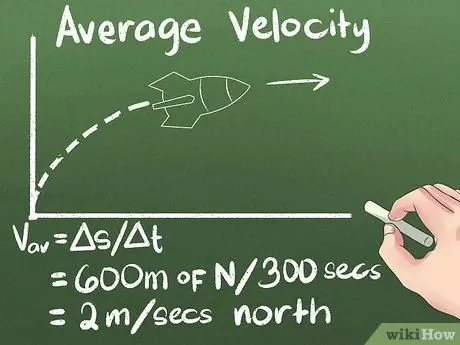
שלב 4. חישוב המהירות הממוצעת כתזוזה לאורך זמן

אם אתה יודע כמה רחוק אובייקט זז, וכמה זמן ייקח להגיע לשם, תדע כמה מהר הוא זז. אז לדוגמא בה אנו משתמשים, המהירות הממוצעת של הרקטה היא (600 מטר צפונה) / (300 שניות) = 2 מטר/שנייה צפונה.

• זכור לכלול כיוון (כגון "חזית" או "צפון").
• בנוסחה v_אָב = s/Δt. סמל הדלתא פירושו "שינוי", ולכן s/Δt פירושו "שינוי המיקום לאורך פרק זמן".
• ניתן לכתוב את המהירות הממוצעת כ- v_אָב, או כ- v עם קו אופקי מעליו.

שלב 5. פתור בעיות מסובכות יותר

אם אובייקט משנה את כיוונו או מהירותו, אל תתבלבלו. המהירות הממוצעת עדיין "רק" מחושבת מתוך העקירה הכוללת והזמן הכולל. מה שקורה בין נקודות ההתחלה והסיום אתה יכול להתעלם. להלן כמה דוגמאות לאובייקט שנסע באותה תזוזה ובזמן הכולל, ובכך אותה מהירות ממוצעת:

• אנה הולכת מערבה במהירות של 1 מטר/שניות למשך 2 שניות, ואז מואצת לפתע ל -3 מטרים/שנייה וממשיכה ללכת מערבה במשך 2 שניות. התזוזה הכוללת היא (1 מ/ש מערבה) (2 שניות) + (3 מ/ש מערבה) (2 שניות) = 8 מטרים מערבה. הזמן הכולל הוא 2 שניות + 2 שניות = 4 שניות. אז המהירות הממוצעת היא 8 מטרים מערבית/ 4 שניות = 2 מטר/שני מערבה.

• בארט הולך מערבה ב -5 מטר/שניות למשך 3 שניות, ואז מסתובב והולך מזרחה ב -7 מטר/שנייה למשך שנייה אחת. אנו יכולים לחשוב על התנועה מזרחה כ"תנועה שלילית מערבה ", כך שהתזוזה הכוללת היא = (5 מטר/שנייה מערבה) (3 שניות) + (-7 מ/ש מערבה) (1 שניות) = 8 מטרים. זמן כולל = 4 שניות. מהירות ממוצעת = 8 מטרים מערבית / 4 שניות = 2 מטר/מערב מערבי.

• שרלוט הלכה צפונה מטר אחד ואז הלכה מערבה 8 מטר, ואז דרומה מטר אחד. הזמן שנדרש להשלמת המסע כולו הוא 4 שניות. צייר את התרשים על פיסת נייר, ותראה שנקודת הסיום נמצאת 8 מטרים ממערב לנקודת ההתחלה, כך שהערך הזה הוא העקירה. הזמן הכולל שלוקח הוא 4 שניות, כך שהמהירות הממוצעת היא 8 מטרים מערבה / 4 שניות = 2 מטר/מערב מערבי.

שיטה 2 מתוך 2: חישוב המהירות הממוצעת של האצה קבועה

שלב 1. שקול את המהירות ההתחלתית והאצה הקבועה

נניח שהבעיה שלנו היא "אופניים נעים ימינה במהירות של 5 מ/ש, עם האצה קבועה של 2 מ/ש². אם האופניים האלה נעים במשך 5 שניות, מה המהירות הממוצעת שלו?"

אם היחידה "מטר/שנייה²"כדי לבלבל אותך, כתוב את זה כ"מטרים/שנייה/שנייה" או "מטר לשנייה לשנייה." האצה של 2 מטר/שנייה/שנייה פירושה שהמהירות עולה בשני מטרים לשנייה בכל שנייה.

שלב 2. השתמש בתאוצה כדי למצוא את המהירות הסופית

האצה, המסומנת בסימון a, היא קצב השינוי של המהירות (או הקצב). המהירות עולה בקצב עלייה קבוע. אתה יכול לצייר טבלה באמצעות האצה כדי למצוא את המהירות בזמנים שונים לאורך מסע האופניים. עלינו ליצור טבלה זו כדי למצוא את נקודת הסיום של הבעיה (ב- t = 5 שניות), אך ניצור טבלה ארוכה יותר כדי להקל עליך להבין את הרעיון הזה:

• בנקודת ההתחלה (זמן t = 0 שניות), האופניים נעים במהירות של 5 מטרים/שניות.
• לאחר שנייה אחת (t = 1), האופניים נעים במהירות של 5 מטר/שנייה + ב = 5 מטר/שנייה + (2 מטרים/שנייה²) (שנייה אחת) = 7 מטרים/שנייה.
• ב t = 2 האופניים נעים ימינה במהירות של 5+ (2) (2) = 9 מטר/שניות.
• ב t = 3 האופניים נעים ימינה במהירות של 5+ (2) (3) = 11 מטר/שניות.
• ב t = 4 האופניים נעים ימינה במהירות של 5+ (2) (4) = 13 מטר/שניות.
• ב t = 5 האופניים נעים ימינה במהירות 5+ (2) (5) = 15 מטר/שנייה.

שלב 3. השתמש בנוסחה זו כדי למצוא את המהירות הממוצעת

אם ו"רק "אם ההאצה קבועה, המהירות הממוצעת תהיה שווה לערך הממוצע של סכום המהירות הסופיות וההתחלתיות. (v_ו +v_אני)/2. לבעיית הדוגמה שלנו למעלה, המהירות ההתחלתית של האופניים היא v_אני 5 מטר/שנייה. לאחר שחשבנו, המהירות הסופית היא v_ו 15 מטר/שנייה. אם מוסיפים את שני הערכים הללו, מקבלים (15 מטר/שנייה + 5 מטר/שנייה)/2 = (20 מטר/שנייה)/2 = 10 מטר/שנייה כיוון ימינה.

• זכור לכלול את הכיוון, במקרה זה "נכון".
• ניתן לכתוב מונח זה כ- v₀ (מהירות בזמן 0, או מהירות התחלתית) ו- v (מהירות סופית).

שלב 4. להבין את נוסחת המהירות הממוצעת באופן אינטואיטיבי

כדי למצוא את המהירות הממוצעת, נוכל להשתמש במהירות בכל נקודה ולמצוא את הממוצע לכולם. (זוהי ההגדרה של ממוצע.) מכיוון שזה דורש חשבון או זמן אינסופי, להבין את הנוסחה הזו בצורה אינטואיטיבית יותר. במקום לקחת כל פעם, חשב את המהירות הממוצעת של שתי נקודות הזמן וראה את התוצאות. נקודת זמן אחת היא סמוך לתחילת הנסיעה, שבה האופניים הולכים לאט, ונקודה נוספת היא סמוך לנקודת הסיום שבה האופניים נוסעים במהירות.

שלב 5. בדוק את התאוריה האינטואיטיבית

השתמש בטבלה למעלה כדי לקבוע את המהירות בנקודות זמן שונות. כמה זוגות שעונים לקריטריונים שלנו הם (t = 0, t = 5), (t = 1, t = 4) או (t = 2, t = 3). אתה יכול לבדוק נוסחה זו עם ערכי t אחרים מלבד מספרים שלמים, אם תרצה.

איזה זוג נקודות שתבחר, המהירות הממוצעת באותו הזמן תמיד תהיה זהה. לדוגמה, ((5+15)/2), ((7+13)/2) או ((9+11)/2) כולם שווים 10 מטר/שנייה מימין

שלב 6. השלם את ההסבר האינטואיטיבי

אם נשתמש בשיטה זו עם רשימה של כל פעם שנלקחה, נמשיך לחשב את ממוצע החצי הראשון של הטיול ואת המחצית השנייה של הטיול. הזמן שלוקח לכסות כל מחצית זהה, כך שאף מהירות לא תאבד כשנסיים לספור.

• מכיוון שכל אחד מהזוגות ייתן את אותה תוצאה, הממוצע של המהירויות הללו יהיה גם זהה בערך. בדוגמה שלנו, מהירות השלם היא "10 מטר/שנייה ימינה" עדיין תהיה 10 מטר/שנייה ימינה.
• אנו יכולים למצוא ערך זה על ידי חישוב הממוצע של כל זוג, למשל המהירות ההתחלתית והסופית. בדוגמה שלנו, מהירויות אלה מגיעות ב t = 0 ו- t = 5, וניתן לחשב אותן באמצעות הנוסחה שלמעלה: (5+15)/2 = 10 מטר/שנייה מימין.

שלב 7. להבין נוסחה זו מבחינה מתמטית

אם נוח לך יותר עם הוכחות שנכתבו כנוסחאות, תוכל להתחיל בנוסחה לחישוב המרחק הנסיעה בהנחה של האצה קבועה, ולגזור משם את הנוסחה:

• s = v_אניt + ב². (מבחינה טכנית s או t, או שינוי מיקום ושינוי בזמן, אבל גם אם תכתוב s ו- t, יבינו אותך.)
• מהירות ממוצעת v_אָב מוגדר כ- s/t, לכן הזן את הנוסחה בטופס s/t.
• v_אָב = s/t = v_אני + ב-
• האצה x זמן שווה לשינוי המהירות הכוללת, או v_ו - v_אני. אז נוכל להחליף את "at" בנוסחה ולקבל:
• v_אָב = v_אני + (v_ו - v_אני).
• לפשט: v_אָב = v_אני + v_ו - v_אני = v_אני + v_ו = (v_ו +v_אני)/2.

טיפים

• מהירות שונה ממהירות מכיוון שהמהירות היא כמות וקטורית ואילו המהירות היא כמות סקלרית. כמויות וקטור כוללות כיוון וגודל כאחד, ואילו כמויות סקלריות כוללות רק גודל.
• אם האובייקט נע בממד אחד, כגון שמאל-ימין, תוכל להשתמש במספר חיובי כדי לייצג כיוון אחד (כגון ימין) ומספר שלילי לייצוג כיוון אחר (שמאל). כתוב את הסימון הזה בראש הדף שלך כך שיהיה ברור לאנשים שקוראים את העבודה שלך.