- מְחַבֵּר Jason Gerald [email protected].
- Public 2024-01-15 08:15.
- שונה לאחרונה 2025-01-23 12:18.
הוספה וחיסור של שברים היא מיומנות חשובה. שברים מופיעים בחיי היומיום כל הזמן, במיוחד בשיעורי מתמטיקה, מהיסודי ועד המכללה. בצע את השלבים הבאים כדי ללמוד כיצד להוסיף ולחסר שברים, משברים שווים, שברים לא שווים, מספרים מעורבים או שברים נפוצים. אם אתה כבר יודע דרך אחת, זה ממש קל לפתור את השברים האחרים!
שלב
שיטה 1 מתוך 4: הוספה וחיסור של שברים באותו מכנה
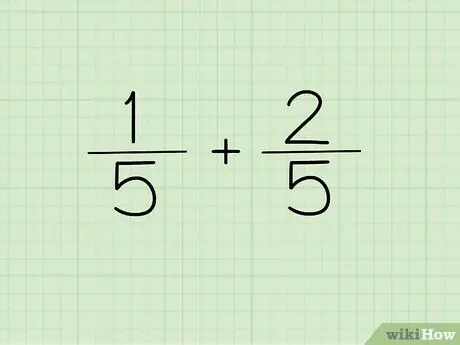
שלב 1. רשום את שאלתך
אם המכנה של שני השברים שברצונך להוסיף או להפחית זהה, רשום את המכנה פעם כמכנה לתשובתך.
במילים אחרות, 1/5 ו- 2/5 לא צריכים להיכתב כ 1/5 + 2/5 =?, אך ניתן לכתוב אותו כ (1+2)/5 =?. המכנים זהים, כך שניתן לכתוב אותם רק פעם אחת. שני המונים משולבים
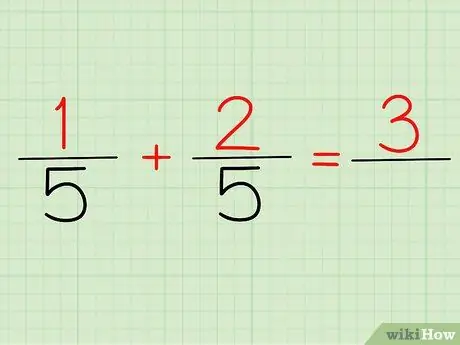
שלב 2. הוסף את המונים
המונה הוא המספר שנמצא מעל כל חלק. אם נסתכל על הבעיה למעלה, 1/5 ו- 2/5, 1 ו- 2 הם המונים שלנו.
בין אם אתה כותב את זה 1/5 + 2/5 או (1 + 2)/5, התשובה שלך תהיה זהה: 3! כי 1 + 2 = 3

שלב 3. עזוב את המכנה
מכיוון שהמכנים זהים, אל תעשה שום דבר עם המכנים! אין להוסיף, לחסר, להכפיל או לחלק. תן לזה להיות.
אז, מאותה דוגמה, המכנה שלנו הוא 5. צודק! 5 הוא המספר התחתון של השבר שלנו. קיבלנו חצי תשובה

שלב 4. רשום את התשובה שלך
כל שעליך לעשות הוא לרשום את המונה והמכנה שלך! אם אתה משתמש בדוגמה למעלה, התשובה שלך תהיה 3/5.
מה המונה שלך? 3. המכנה שלך? 5. לכן, 1/5 + 2/5 או (1 + 2)/5 שווה ל- 3/5.
שיטה 2 מתוך 4: הוספה וחיסור של שברים עם מכנים שונים

שלב 1. מצא את המכנה הכי פחות משותף
כלומר, המכנה הקטן ביותר זהה לשני השברים. נניח שיש לנו את השברים 2/3 ו -3/4. מהו המכנה? 3 ו 4. כדי למצוא את המכנה הפחות משותף של שני השברים, תוכל לעשות זאת בשלוש דרכים:
- רשום את הכפלות של. כפולים של 3 הם 3, 6, 9, 12, 15, 18 … וכן הלאה. כפולות של 4? 4, 8, 12, 16, 20 וכן הלאה. מהו המספר הקטן ביותר שמכפיל את השניים? 12! זה המכנה הכי פחות משותף.
-
פירוק לגורמים ראשוניים. אם אתה יודע על גורמים, אתה יכול לבצע פקטוריזציה ראשונית. כלומר, אתם מחפשים את המספרים המרכיבים את המכנה שלכם. עבור המספר 3, הגורמים הם 3 ו -1 עבור המספר 4, הגורמים הם 2 ו 2. לאחר מכן, כולכם. 3 x 2 x 2 = 12. המכנה הכי פחות משותף שלכם!
הכפל את כל המספרים למספר הקטן יותר. בכמה בעיות, כמו זו, אתה יכול להכפיל את שני המספרים - 3 x 4 = 12. עם זאת, אם יש לך מכנה גדול, אל תעשה זאת! אתה לא רוצה להכפיל 56 על 44 ולצאת על הכל כדי לקבל 2,464

שלב 2. הכפל את המכנה במספר הדרוש בכדי לקבל את המכנה המשותף הקטן ביותר
במילים אחרות, אתה רוצה שכל המכנים שלך יהיו שווים. בדוגמה שלנו, אנו רוצים שהמכנה יהיה 12. כדי לשנות 3 ל -12, אתה מכפיל 3 ב -4. כדי לשנות 4 ל -12, אתה מכפיל 4 ב 3. אותו מכנה יהיה המכנה של התשובה הסופית שלך.
-
אז 2/3 הופך 2/3 x 4 ו 3/4 הופך 3/4 x 3. כלומר, עכשיו יש לנו 2/12 ו 3/12. אבל, עדיין לא סיימנו!
- תבחין כי המכנים מכופלים זה בזה. ניתן לעשות זאת במצב זה, אך לא בכל המצבים. לפעמים, במקום להכפיל את שני המכנים, אתה יכול להכפיל את שני המכנים במספר אחר כדי לקבל את המספר הקטן יותר.
- ואז בבעיות אחרות, לפעמים אתה רק צריך להכפיל מכנה אחד כדי להפוך אותו למכנה של השבר השני בבעיה.

שלב 3. הכפל את המונה באותו מספר
כאשר אתה מכפיל את המכנה במספר, עליך גם להכפיל את המונה באותו מספר. מה שעשינו בשלב האחרון הוא רק חלק מהריבוי שיש לעשות.
יש לנו 2/3x4 ו 2/4x3 כצעד הראשון - ואז, בשלב השני, 2 x 4/3 x 4 ו- 3 x 3/4 x 3. כלומר, המספרים החדשים שלנו הם 8/12 ו- 9/ 12. מושלם
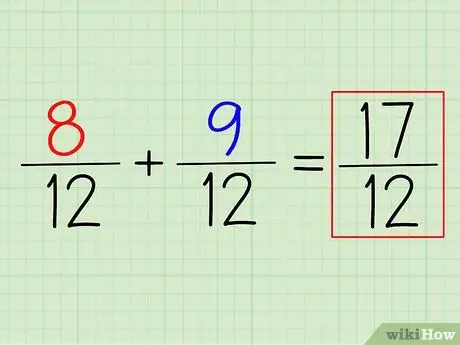
שלב 4. הוסף (או הפחת) את המונים כדי לקבל את התשובה
כדי להוסיף 8/12 + 9/12, כל שעליך לעשות הוא להוסיף את המונים. זכרו: פשוט עזבו את המכנה. המכנה המשותף הקטן ביותר שתמצא הוא המכנה הסופי שלך.
בדוגמה זו, (8+9)/12 = 17/12. כדי להמיר אותו למספר מעורב, פשוט הפחת את המכנה מהמונה והרשום את השאר. במקרה זה, 17/12 = 1 5/12
שיטה 3 מתוך 4: הוספה והסרה של שברים מעורבים ושכיחים
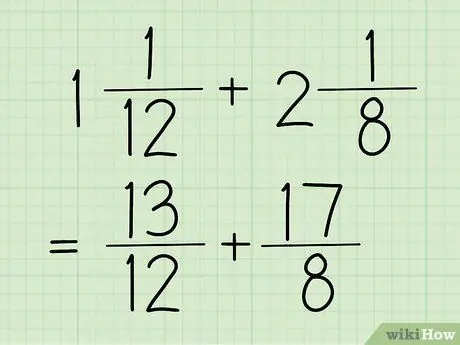
שלב 1. המיר את השברים המעורבים שלך לשברים נפוצים
מספר מעורב הוא שבר בעל מספר שלם ושבר, כמו בדוגמה למעלה (1 5/12). בינתיים, שבר רגיל הוא שבר שמספרו (המספר העליון) גדול מהמכנה (המספר התחתון). חלק זה נראה גם בשלב הקודם, שהוא 17/12.
עבור הדוגמאות בסעיף זה, נשתמש ב -13/12 וב -17/8

שלב 2. מצא מכנה משותף
אתה זוכר את שלוש הדרכים למצוא את המכנה הכי פחות משותף? על ידי כתיבת מכפילים, שימוש בגורם ראשוני או הכפלת המכנים.
בואו למצוא כפולים של הדוגמא שלנו, 12 ו- 8. מהו המספר הקטן ביותר המשותף לשניהם? 24. 8, 16, 24, ו -12, 24 - בינגו

שלב 3. הכפל את המונה והמכנה שלך כדי למצוא את השבר המקביל
יש לשנות את שני המכנים ל- 24. איך ממירים 12 ל -24? להכפיל ב- 2. 8 עד 24? הכפל בשלוש. אך אל תשכח - עליך להכפיל גם את המונים!
אז (13 x 2)/(12 x 2) = 26/24. וגם (17 x 3)/(8 x 3) = 51/24. כמעט סיימנו עם זה

שלב 4. הוסף או הפחת את השברים שלך
עכשיו כשיש לך אותו מכנה, אתה יכול בקלות להוסיף את שני המונים יחד. זכור, פשוט עזוב את המכנה!
26/24 + 51/24 = 77/24. זה הסכום שלך! עם זאת, המספרים בחלק העליון היו גדולים מדי …

שלב 5. החזר את התשובה שלך למספרים מעורבים
המספר הגדול מאוד בחלק העליון של השבר מרגיש קצת מוזר - אי אפשר לדעת את גודל השבר שלך. כל שעליך לעשות הוא להפחית את המכנה שלך מן המונה שוב ושוב עד שלא ניתן להחסיר אותו יותר ולרשום את השאר.
-
בדוגמה זו, 77 מינוס 24 על 3 פעמים. כלומר, 24 x 3 = 72. השאר הוא 5! אז מה התוצאה הסופית שלך? 3 5/24.
כל כך נכון!
שיטה 4 מתוך 4: הוסף וחסר שברים מבלי למצוא LCM
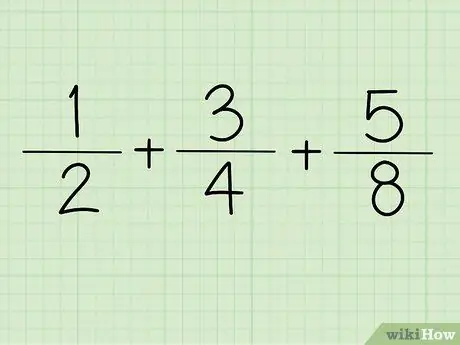
שלב 1. רשום את השבר
למשל + +

שלב 2. קודם כל תפתור את המונה
- הכפל במספר השבר השני.
- כפל 1 על 4 ו- 8. [32]
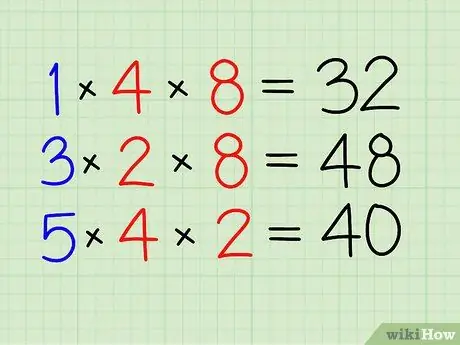
שלב 3. עשו את אותו הדבר לגבי השברים האחרים
- כפל 3 על 2 ו- 8. [48]
- לבסוף, כפל 5 ב- 4 ו- 2. [40]
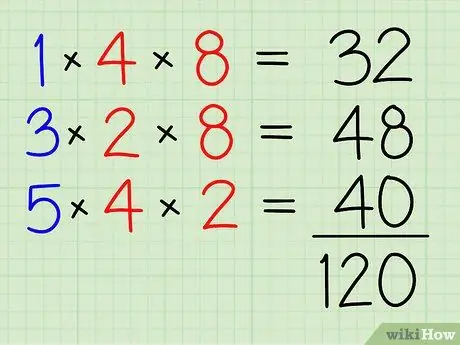
שלב 4. מוסיפים את כולם יחד
32+48+40=120
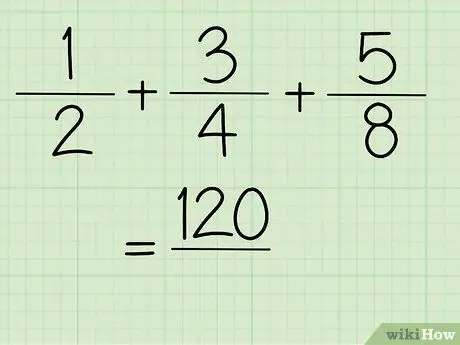
שלב 5. כעת, אתה מקבל את ערך המונה

שלב 6. פתרו את המכנה של השבר

שלב 7. הכפל את כל המכנים של השברים
2×4×8=64

שלב 8. עכשיו, אתה מקבל את התוצאה
120/64 = 1 56/64 = 1 ⅞
אַזהָרָה
- שיטה זו מאפשרת לך להכפיל מספרים גדולים.
- ייתכן שתזדקק למחשבון בכדי לחשב זאת.






