הממוצע הגיאומטרי הוא דרך נוספת למצוא את הערך הממוצע של קבוצת מספרים, הנעשית על ידי הכפלת הערכים לפני נטילת השורשים, במקום חיבור הערכים וחילוקם כמו בממוצע אריתמטי. ניתן להשתמש בממוצע הגיאומטרי לחישוב שיעור התשואה הממוצע בניתוח פיננסי או להצגת קצב הצמיחה של משהו לאורך תקופה. כדי למצוא את הממוצע הגיאומטרי, הכפל את כל הערכים לפני השתרשות ב, שהוא המספר הכולל של המספרים במערך. תוכל גם להשתמש בפונקציית הלוגריתם במחשבון שלך כדי למצוא את הממוצע הגיאומטרי, אם אתה מעדיף.
שלב
שיטה 1 מתוך 2: מציאת הממוצע הגיאומטרי של קבוצת ערכים
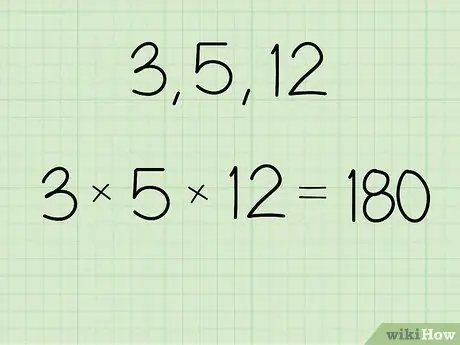
שלב 1. הכפל את הערך שלשמו ברצונך למצוא את הממוצע הגיאומטרי
אתה יכול להשתמש במחשבון או לחשב ידנית כדי לקבל את התוצאה. רשמו את התוצאות כדי שלא תשכחו.
- לדוגמה, אם קבוצת המספרים היא 3, 5 ו -12, חשבו: (3 x 5 x 12) = 180.
- לדוגמא נוספת, אם ברצונך למצוא את הממוצע הגיאומטרי של קבוצת המספרים 2 ו -18, כתוב: (2 x 18) = 36.
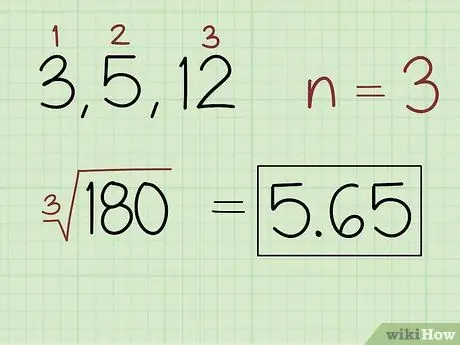
שלב 2. מצא את השורש ה- n של המוצר, כאשר n הוא מספר הערכים במערך
ספרו את מספר המספרים בסט כדי לקבל את הערך. השתמש בערכים כדי לציין את השורש שצריך להשתמש בו במוצר. לדוגמה, השתמש בשורש הריבועי אם הערכה מכילה 2 מספרים, השורש המעוקב אם הערכה מכילה 3 מספרים וכן הלאה. השתמש במחשבון כדי לפתור את המשוואה ולרשום את התשובה.
- לדוגמה, עבור קבוצת מספרים 3, 5 ו -12 כתוב: (180) 5, 65.
- בדוגמה השנייה עם הסט המכיל 2 ו -18, כתוב: (36) = 6.
וָרִיאַצִיָה:
תוכל גם לכתוב את השורש כמעריך של 1/, אם קל יותר לכתוב על מחשבון. לדוגמה, עבור קבוצת המספרים 3, 5 ו -12, כתוב (180)1/3 במקום (180).
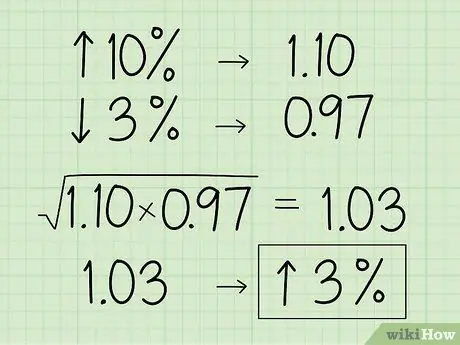
שלב 3. המר את האחוזים למקביל המכפיל העשרוני שלו
אם קבוצת המספרים כתובה כעלייה או ירידה באחוזים, נסה לא להשתמש בערך האחוז בממוצע הגיאומטרי מכיוון שהתוצאות לא יהיו מדויקות. אם האחוז עולה, הזז את הנקודה העשרונית שתי ספרות שמאלה והוסף 1. אם האחוז יורד, העבר את הנקודה העשרונית 2 ספרות שמאלה וחסר מ -1.
- לדוגמה, נניח שאתה רוצה למצוא את הממוצע הגיאומטרי של ערכי האובייקט שעולה ב -10%ואז יורד ב -3%.
- המר 10% למספר עשרוני והוסף 1 כדי לקבל 1, 10.
- לאחר מכן, המירו 3% למספר עשרוני וחסרו 1 כדי לקבל 0.97.
- השתמש בשני המקומות העשרוניים כדי למצוא את הממוצע הגיאומטרי: (1, 10 x 0.97) 1.03.
- המרת המספר בחזרה לאחוז על ידי הסטת הנקודה העשרונית ב -2 ספרות ימינה וחסרת 1 כדי לקבל עלייה בערך של 3%.
שיטה 2 מתוך 2: חישוב הממוצע הגיאומטרי באמצעות לוגריתמים
שלב 1. הוסף את הערכים הלוגריתמיים לכל מספר במערך
הפונקציה LOG במחשבון לוקחת את בסיס 10 של מספר וקובעת כמה אתה צריך להכפיל ב- 10 כך שזה ישתווה למספר. חפש את הפונקציה LOG במחשבון, הנמצא בדרך כלל בצד שמאל של הכפתור. לחץ על כפתור LOG והזן את המספר הראשון בערכה. הקלד "+" לפני הזנת LOG עבור המספר השני. המשך להפריד בין פונקציית LOG לכל מספר באמצעות סמל פלוס לפני קבלת הסכום.
- לדוגמה, עבור ערכות 7, 9 ו -12, הקלד log (7) + log (9) + log (12), ולאחר מכן הקש "=" במחשבון. אם הפונקציה חושבה, המספר יהיה סביב 2.878521796.
- ניתן גם לחשב כל לוגריתם בנפרד לפני הוספת כולם יחד.
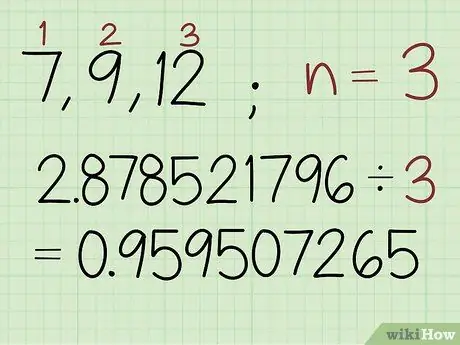
שלב 2. חלק את סכום הערכים הלוגריתמיים במספר המספרים במערך
ספור את מספר הערכים במערך וחלק את המספר שהתקבל בעבר במספר זה. התוצאה היא הלוגריתם של הממוצע הגיאומטרי.
בדוגמה זו, ישנם 3 מספרים במערך כך הקלד: 2, 878521796 /3 0, 959507265
שלב 3. מצא את האנטי -לוג של המנה כדי לקבוע את הממוצע הגיאומטרי
פונקציית האנטי -לוג היא ההיפוך של פונקציית LOG במחשבון וממיר את הערך חזרה לבסיס 10. חפש את הסמל "10איקס”במחשבון, שהוא בדרך כלל פונקציה משנית של לחצן LOG. לחץ על כפתור "2" בפינה השמאלית העליונה של המחשבון ואחריו על כפתור LOG להפעלת האנטי -לוג. הקלד את המנה שנמצאה בשלב האחרון לפני פתרון המשוואה.
בדוגמה זו, המחשבון יציג: 10(0, 959507265) ≈ 9, 11.
טיפים
- אינך יכול למצוא את הממוצע הגיאומטרי של מספרים שליליים.
- לכל הסטים שיש להם 0 יהיה ממוצע גיאומטרי של 0.
