- מְחַבֵּר Jason Gerald [email protected].
- Public 2024-01-15 08:15.
- שונה לאחרונה 2025-01-23 12:18.
ישנן דרכים שונות לבצע את החלוקה. אתה יכול לחלק עשרונים, שברים או אפילו מעריכים ולהשתמש בחלוקה ארוכה או קצרה. אם אתה רוצה לדעת את הדרכים השונות לחלוקת מספרים, בצע את השלבים שלהלן.
שלב
שיטה 1 מתוך 5: ביצוע חטיבה של סדרות ארוכות

שלב 1. רשום את השאלות
כדי לבצע חלוקה ארוכה, מקם את המכנה (המספר שיחלק) מחוץ לסרגל המחלק, ואת המונה (המספר שיש לחלק) בתוך סרגל המחלק.
לדוגמה: 136 ÷ 3

שלב 2. חלק את הספרה הראשונה של המונה במכנה (במידת האפשר)
בדוגמה זו, 1 אינו מתחלק ב -3 אז שים 0 מעל סרגל המחלק ועבור לשלב הבא. מחסירים 1 על 0 ומכניסים את התוצאה למספר 1.

שלב 3. חלק את מספר שאר הספרה הראשונה של המונה ואת הספרה השנייה של המונה על ידי המכנה
מכיוון שלא ניתן לחלק את 1 ב -3, המספר 1 עדיין בשימוש. עליך לחסר 3. כעת, חלק את 13 ב- 3. מכיוון ש -3 x 4 = 12, שים את 4 מעל סרגל המחלק (מימין ל -0), ולאחר מכן הפחת 13 על 12 וכתוב את התוצאה מתחתיו.

שלב 4. חלק את המספרים הנותרים במכנה
הורד את המספר 6 מימין ל -1, כדי לקבל 16. כעת, חלק את 16 ב- 3. מאחר 3 x 5 = 15, כתוב את המספר 5 מימין למספר 4, וחסר 16 ב- 15 וכתוב את התוצאה (16-15 = 1) מתחתיו.

שלב 5. כתוב את השאר ליד המנה
התשובה הסופית שלך היא 45 עם אחד שנותר, או 45 R1.
שיטה 2 מתוך 5: ביצוע חטיבות קצרות

שלב 1. רשום את השאלות
כתוב את המכנה (המספר שיש לחלק) מחוץ לשורת המחלק, ואת המונה (המספר שיש לחלק) בתוך סרגל המחלק. שים לב שבחלוקה קצרה המכנה אינו יכול להיות יותר מספר אחד.
לדוגמה, 518 4

שלב 2. חלק את הספרה הראשונה של המונה במכנה
5 4 = 1 R1. מקם את המנה (1) מעל סרגל המחיצה הארוך. כתוב את השאר מעל הספרה הראשונה של המונה. מקם 1 על 5 קטן כדי להזכיר לך שנשאר לך 1 כשאתה מחלק את 5 ב -4. 518 אמור להיראות כך: 5118

שלב 3. חלק את המספר שנוצר מהיתר ואת הספרה השנייה של המונה על ידי המכנה
המספר הבא הוא 11 המתקבל מהערך השיורי (1) ומהספרה השנייה של המונה (1). 11 4 = 2 R 3 כי 4 x 2 = 8 עם שארית 3. כתוב את ערך השיור מעל הספרה השנייה של המונה. שים 3 על 1. המונה הראשוני (518) נראה כעת כך: 51138

שלב 4. חלק את המספרים הנותרים על ידי המכנה
המספר הנותר הוא 38; המספר 3 מגיע משאר השלב הקודם, ו -8 הוא הספרה האחרונה של המונה. חשב 38 4 = 9 R2. מכיוון ש -4 x 9 = 36, כתוב "R2" מעל סרגל החלוקה כי 38 - 36 = 2.

שלב 5. רשמו את התשובה הסופית
התוצאה הסופית והכמות נמצאים מעל סרגל המחלק. התשובה היא 518 4 = 129 R2.
שיטה 3 מתוך 5: חלקים שברים

שלב 1. רשום את השאלות
כדי לחלק שבר, פשוט רשום את השבר הראשון ואחריו סמל החלוקה ולאחר מכן את השבר השני.
לדוגמא: 3/4 5/8

שלב 2. הפוך את המונה והמכנה של השבר השני
השבר השני הוא כעת הדדי.
דוגמא: 3/4 8/5

שלב 3. שנה את סמל החלוקה לסמל הזמנים
כדי לחלק שבר, אתה מכפיל את השבר הראשון בהדדי של השני.
דוגמה: 3/4 x 8/5
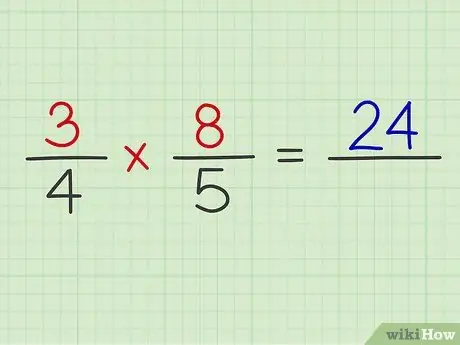
שלב 4. הכפל את המונה של שני השברים
פשוט עשה זאת כמו להכפיל שני שברים רגילים.
דוגמה: 3 x 8 = 24
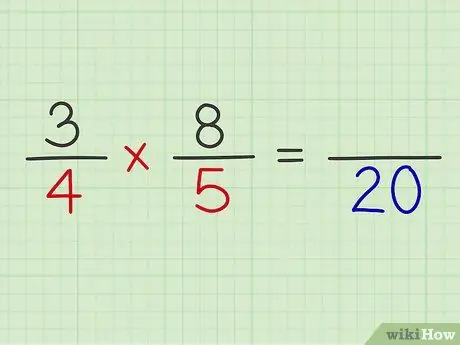
שלב 5. הכפל את המכנים של שני השברים
השלם את החישוב על ידי הכפלת שני השברים.
דוגמה: 4 x 5 = 20
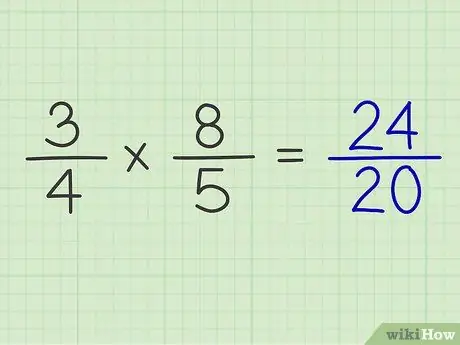
שלב 6. שים את המוצר של המונה מעל המוצר של המכנה
לאחר הכפלת המונה והמכנה של שני השברים, תוכל לקבל את התוצאה של חישוב שני השברים.
דוגמה: 3/4 x 8/5 = 24/20

שלב 7. פשט שברים
כדי למצוא את הגורם המשותף הגדול ביותר, או את המספר הגדול ביותר המחלק את המונה והמכנה באופן שווה. במקרה זה, הגורם המשותף הגדול ביותר בין 24 ו -20 הוא 4. על מנת להוכיח זאת, רשום את כל המונים והמכנים, והקיף את מספר הגורמים הנפוצים הגדולים ביותר של שניהם.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- מכיוון ש -4 הוא הגורם המשותף הגדול ביותר של 24 ו -20, פשוט חלק את שני המספרים ב -4 כדי לפשט את השבר.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

שלב 8. שכתב את השבר כמספר מעורב (אופציונלי)
הטריק, פשוט חלק את המונה במכנה, וכתוב את התוצאה כמספר שלם. לאחר מכן כתוב את שאר החלוקה כמניין חדש, ומכנה השבר אינו משתנה. מכיוון ש -6 מחולקים ב -5 תוצאות ב -1 עם שארית 1, כתוב את כל המספר 1, ואחריו את המונה החדש 1, ואז המכנה 5 כדי לקבל מספר מעורב 1 1/5.
דוגמא: 6/5 = 1 1/5
שיטה 4 מתוך 5: חלוקת מעריך

שלב 1. ודא שלמעריכים/כוחות יש אותו מספר בסיס
אתה יכול לחלק רק מעריכים אם יש להם אותו מספר בסיס. אחרת, תוכל לנסות לתפעל אותם עד שתקבל אותו מספר בסיס.
דוגמה: x8 איקס5

שלב 2. הפחת את המעריך
אתה יכול פשוט להפחית את המעריך הראשון בשני. לא אכפת לך מהמספרים הבסיסיים בינתיים.
דוגמה: 8 - 5 = 3
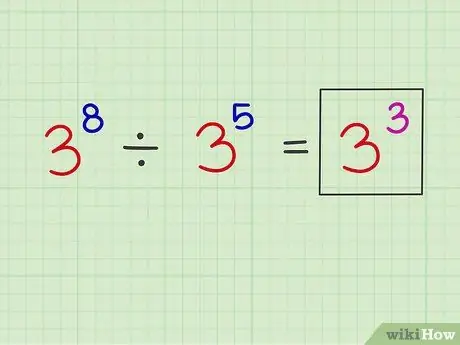
שלב 3. הנח את המעריך החדש מעל מספר הבסיס המקורי
כעת תוכל לכתוב את המעריך החדש על פני מספר הבסיס המקורי.
דוגמה: x8 איקס5 = x3
שיטה 5 מתוך 5: חלוקת מספרים עשרוניים

שלב 1. רשום את השאלות
כתוב את המכנה (המספר שיש לחלק) מחוץ לשורת המחלק, ואת המונה (המספר שיש לחלק) בתוך סרגל המחלק. בחלוקה עשרונית, המטרה שלך היא להמיר מספר עשרוני למספר שלם.
דוגמה: 65.5.5

שלב 2. שנה את המכנה למספר שלם
פשוט החלק את הנקודה העשרונית במספר אחד ימינה כדי לשנות 0.5 ל -5, aka 5, 0.

שלב 3. שנה את המונה על ידי הסטת הנקודה העשרונית באותו מספר ספרות כמו המכנה
מכיוון שאתה מזיז את הנקודה העשרונית של המונה ספרה אחת ימינה כך שהוא הופך למספר שלם, הנקודה העשרונית של המכנה מועברת גם ספרה אחת ימינה כך ש- 65.5 משתנה ל -655.
אם אתה מעביר את הנקודה העשרונית של המונה מעבר לכל הספרות שלו, זה אומר שאתה צריך להוסיף אפסים למספרים בכל פעם שהנקודה העשרונית תועבר. לדוגמה, אם הנקודה העשרונית 7, 2 מועברת שלוש ספרות ימינה, המספר משתנה ל -7,200 מכיוון שהמרווח הריק בן שתי הספרות מלא באפסים

שלב 4. הנח את הנקודה העשרונית בסרגל החלוקה הארוכה ממש מעל לנקודה העשרונית במניין
מכיוון שאתה מעביר את הנקודה העשרונית במספר אחד כדי להפוך 0.5 למספר שלם, מומלץ למקם את הנקודה העשרונית מעל סרגל החלוקה בדיוק למקום בו הנקודה העשרונית נעה, כלומר אחרי ה -5 האחרונות ב -655.

שלב 5. פתור את הבעיה בעזרת חלוקה ארוכה פשוטה
כדי לחלק את 655 ב -5, השלבים הם:
- חלק את מספר הספרות של המונה (6) במכנה (5). התוצאה היא 1 עם שארית 1. כתוב את המספר 1 מעל סרגל המחלק, וכתוב 5 מתחת למספר 6 שיש להפחית.
- שארית ה -1 מופחתת מהספרה העשרות של המונה (5) כך שתקבל כעת 15. חלק 15 ב -5 כדי לקבל 3. כתוב 3 מעל פס המחלק, מימין ל -1.
- שחרר את 5 הספרות האחרונות. חלקו 5 ב -5 כדי לקבל 1. כתבו את המספר 1 מעל סרגל המחלק, מימין למספר 3. אין שארית כי 5 מתחלק ב- 5.
- התשובה הארוכה של חלוקה רציפה היא 655 5 = 131. תוצאה זו זהה לתשובה לשאלות 65.5 0.5.






