בסטטיסטיקה, הטווח הוא ההבדל בין הערך הגבוה ביותר במערך נתונים לבין הערך הנמוך ביותר במערך נתונים. טווח מראה עד כמה הערכים פרוסים בסדרה. אם הטווח הוא מספר גדול, אז הערכים בסדרה מפוזרים מאוד; אם הטווח הוא מספר קטן, אז הערכים בסדרה קרובים זה לזה. אם אתה רוצה לדעת כיצד לחשב את טווח ההגעה, בצע את השלבים הבאים.
שלב
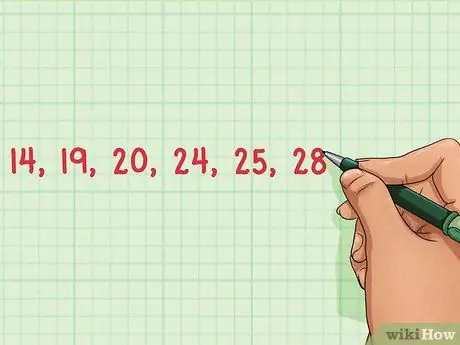
שלב 1. רשום את מרכיבי מערך הנתונים שלך
כדי למצוא את הטווח של מערך נתונים, עליך לרשום את כל האלמנטים במערך הנתונים כך שתוכל לזהות את המספרים הגדולים והקטנים ביותר. רשום את כל האלמנטים. המספרים במערך הנתונים הזה הם: 14, 19, 20, 24, 25 ו -28.
- קל יותר לזהות את המספרים הגדולים והקטנים ביותר במערך נתונים אם מזמינים את המספרים מהקטן לגדול. בדוגמה זו מערכת הנתונים תהיה בנויה כך: 14, 19, 20, 24, 24, 25, 28.
- מיון האלמנטים במערך נתונים יעזור לך גם לבצע חישובים אחרים, כגון מציאת המצב, הממוצע או החציון של מערך הנתונים.
שלב 2. זיהוי המספרים הגדולים והקטנים ביותר במערך הנתונים
בבעיה זו, המספר הקטן ביותר במערך הנתונים הוא 14 והמספר הגדול ביותר הוא 28.
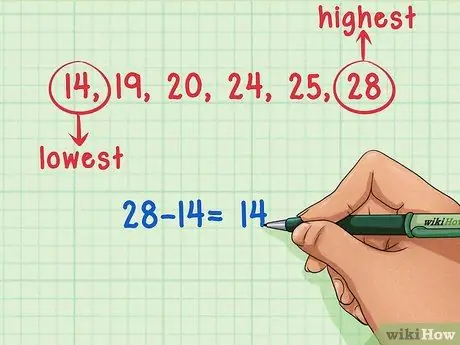
שלב 3. הפחת את המספר הקטן ביותר במערך הנתונים שלך מהמספר הגדול ביותר
כעת, לאחר שזיהית את המספרים הקטנים והגדולים ביותר במערך הנתונים, כל שעליך לעשות הוא להפחית אותם זה מזה. הפחת 14 מ- 25 (25 - 14) כדי לקבל 11, טווח מערך הנתונים.
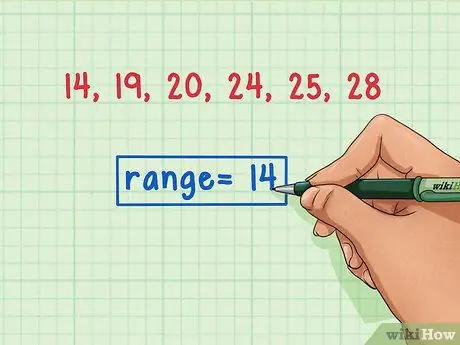
שלב 4. תייג את הטווח בצורה ברורה
לאחר שתמצא את הטווח, סמן אותו בבירור. זה יעזור לך להימנע מבלבול עם חישובים סטטיסטיים אחרים שתצטרך לבצע, כגון מציאת החציון, המצב או הממוצע.
טיפים
- אתה יכול גם לפרש טווח במונחים אלגבריים, אך תחילה עליך להבין את המושג פונקציה אלגברית, או קבוצת פעולות על מספרים ידועים. מכיוון שניתן לבצע פעולות פונקציה בכל מספר, אפילו במספר לא ידוע, המספר מסומן במשתנה אותיות, בדרך כלל x. דומיין הוא קבוצה של ערכי קלט אפשריים, אותם תוכל להחליף את המספר הלא ידוע. לפיכך, הטווח הוא קבוצת תוצאות החישוב האפשריות, שתקבל לאחר הזנת אחד מערכי הדומיין והשלמת כל הפעולות שהוגדרו על ידי הפונקציה. למרבה הצער, אין דרך לחשב את טווח הפונקציה. לפעמים, גרף של פונקציה או חישוב ערכים מרובים יכול להראות דפוס ברור. תוכל גם להשתמש בידע שלך על התחום של הפונקציה כדי למחוק ערכי פלט (תוצאות חישוב), או לצמצם את מערך הנתונים המייצג את הטווח.
- הערך החציוני של כל מערך נתונים סטטיסטי מייצג את הערך החציוני של מערך הנתונים במונחים של חלוקת נתונים, לא טווח. אז למרות שתרצה להניח שהחציון של מערך נתונים נתון הוא הטווח המחולק ב 2 - או חצי מהטווח של הטווח - זה בדרך כלל לא נכון. כדי למצוא את החציון הנכון, עליך למיין את רכיבי הנתונים ולאחר מכן לחפש את הרכיב באמצע הרשימה. אלמנט זה הוא החציון. לדוגמה, אם יש לך רשימה של 29 אלמנטים, לרכיב ה -15 יש אותו טווח מתחילת הרשימה וסוף הרשימה, כך שהרכיב ה -15 הוא החציון, ללא קשר לאופן שבו הערך של אותו אלמנט מתייחס הטווח.
