- מְחַבֵּר Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:13.
- שונה לאחרונה 2025-01-23 12:18.
עקירה בפיסיקה מציינת שינוי במיקום של אובייקט. כאשר אתה מחשב תזוזה, אתה מחשב כמה רחוק אובייקט מבוסס על המיקומים הראשוניים והאחרונים שלו. הנוסחה שבה אתה משתמש לחישוב העקירה תלויה במשתנה שניתן לבעיה. בצע את השלבים הבאים לחישוב העקירה.
שלב
חלק 1 מתוך 5: חישוב העקירה המתקבלת

שלב 1. השתמש בנוסחת העקירה המתקבלת אם יחידת המרחק משמשת לציון מיקומי ההתחלה והסיום שלך
למרות שהמרחק שונה מהתזוזה, בעיית העקירה כתוצאה מכך מחפשת כמה קילומטרים או מטרים חפץ עבר. תוכל להשתמש ביחידת מדידה זו כדי לחשב את העקירה ובאיזה מרחק מיקום החפץ חורג מנקודת ההתחלה שלו.
- נוסחת העקירה המתקבלת כתובה כך: S = x²+y². S היא תזוזה. X הוא כיוון התנועה הראשון של האובייקט ו- Y הוא כיוון התנועה השני של האובייקט. אם האובייקט נע רק בכיוון אחד, אז Y = 0.
- עצם יכול לנוע רק לשני כיוונים לכל היותר מכיוון שנעה לאורך ציר צפון/דרום או מזרח/מערב נחשבת לתנועה ניטרלית.

שלב 2. חבר את הנקודות לפי סדר התנועה וסמן אותן מ- A-Z
השתמש בסרגל כדי לצייר קו ישר מנקודה לנקודה.
- זכור גם לחבר את נקודת ההתחלה שלך לנקודת הסיום שלך באמצעות קו ישר. זוהי העקירה שנחשב.
- לדוגמה, אם עצם נע מזרחה 300 מ 'וצפון 400 מ', הוא יהווה משולש ימני. AB תהיה הרגל הראשונה של המשולש, ו- BC תהיה הרגל השנייה. AC יהיה ההיפנוזה של המשולש וגודלו הוא תזוזה של האובייקט. בדוגמה זו שני הכיוונים הם מזרח וצפון.

שלב 3. הזן ערכים עבור x² ו- y²
כעת, לאחר שאתה מכיר את שני כיווני התנועה של האובייקט שלך, הכנס את הערכים למשתנים המתאימים.
לדוגמה, x = 300 ו- y = 400. הנוסחה שלך צריכה להיראות כך: S = 300² + 400²
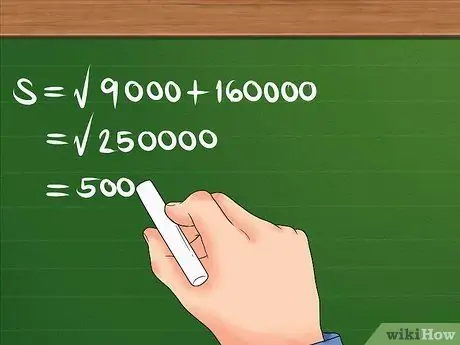
שלב 4. חישוב הנוסחה לפי סדר הפעולות
קודם כל ריבועים 300 ו -400 ואז מוסיפים אותם ומוצאים את השורש הריבועי של הסכום.
לדוגמה: S = 90000 + 160000. S = 250000. S = 500. עכשיו אתה יודע שהתזוזה היא 500 מ '
חלק 2 מתוך 5: כאשר מהירות וזמן ידועים

שלב 1. השתמש בנוסחה זו כאשר הבעיה מספרת לך את מהירות האובייקט ואת הזמן הנדרש
כמה בעיות במתמטיקה לא יגידו לך כמה רחוק או כמה מהר אובייקט נע. אתה יכול לחשב את העקירה בעזרת גודל הזמן והמהירות האלה.
-
במקרה זה, הנוסחה הופכת להיות: S = 1/2 (u + v) t.
U = מהירות התחלתית של האובייקט, או כמה מהר האובייקט מתחיל לנוע בכיוון מסוים. V = מהירותו הסופית של האובייקט, או כמה מהירות האובייקט נע לכיוון מיקומו הסופי. T = הזמן שלוקח לאובייקט להגיע למיקומו הסופי.
- דוגמה: מכונית יורדת לכביש למשך 45 שניות (זמן נדרש). המכונית פונה מערבה ב 20 מ '/ש' (מהירות התחלתית) ובסוף הכביש מהירותה 23 מ '/ש' (מהירות סופית). חשב את העקירה בהתבסס על גורמים אלה.

שלב 2. הזן את המהירות והזמן הנדרשים לתוך המשתנים המתאימים
עכשיו שאתה יודע כמה רחוק המכונית נעה, כמה מהר המכונית נעה בתחילת ובסוף, תוכל למצוא את המרחק ממיקום ההתחלה למיקום הסופי.
הנוסחה שלך צריכה להיראות כך: S = 1/2 (20 + 23) 45

שלב 3. חישוב הנוסחה לאחר הצבת הערכים במקום הנכון
זכור לעקוב אחר סדר הפעולות, אחרת התזוזה תביא לערכים שונים מאוד.
- לנוסחה זו, לא משנה אם תחליף בטעות את מהירות ההתחלה והסיום. מכיוון שתוסיף את המספרים האלה תחילה, לא משנה היכן הם נמצאים בסוגריים. עם זאת, בנוסחאות אחרות, החלפת המהירות ההתחלתית והאחרונה תגרום לערכי תזוזה שונים.
- הנוסחה שלך צריכה להיראות כך: S = 1/2 (43) 45. תחילה נחלק 43 ב -2, מה שמביא ל 21, 5. לאחר מכן הכפל 21, 5 ב -45, כך שהתוצאה היא 967.5 מטר. 967, 5 הוא גודל העקירה שלך, או כמה רחוק המכונית שלך זזה מנקודת ההתחלה שלה.
חלק 3 מתוך 5: כאשר המהירות הראשונית, ההאצה והזמן ידועים
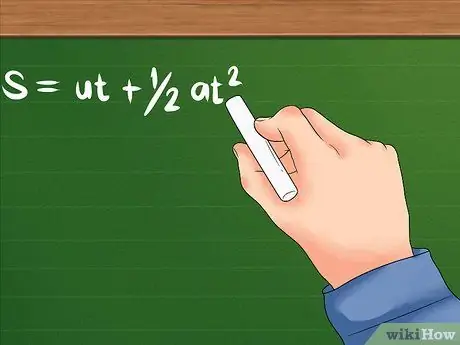
שלב 1. השתמש בנוסחה שהשתנתה כאשר ההאצה ידועה בנוסף למהירות הראשונית והזמן
כמה שאלות רק יגידו לך כמה מהר האובייקט נע בהתחלה, כמה מהר האובייקט מתחיל להאיץ וכמה רחוק האובייקט נע. תזדקק לנוסחה הבאה.
- הנוסחה לבעיה זו היא: S = ut + 1/2at². U עדיין מציין את המהירות ההתחלתית; a היא האצת האובייקט, או כמה מהר מהירותו מתחילה להשתנות. T יכול להיות הזמן שנדרש או פרק זמן מסוים שלוקח לאובייקט להאיץ. שניהם ישתמשו ביחידות זמן כגון שניות, שעות ואחרות.
- נניח שמכונית הנעה במהירות 25 מ '/ש' (מהירות ראשונית) מתחילה להאיץ במהירות של 3 מ '/ש' (האצה) למשך 4 שניות (זמן). מהו העקירה של המכונית לאחר 4 שניות?

שלב 2. הזן את הערכים בנוסחה
שלא כמו הנוסחה הקודמת, רק המהירות ההתחלתית מיוצגת כאן, לכן הקפד להזין את הנתונים הנכונים.
בהתבסס על נתוני המדגם למעלה, הנוסחה שלך תיראה כך: S = 25 (4) + 1/2 (3) 4². זה עוזר להוסיף סוגריים סביב גודל ההאצה והזמן שלך כדי לעזור לך להפריד את המספרים
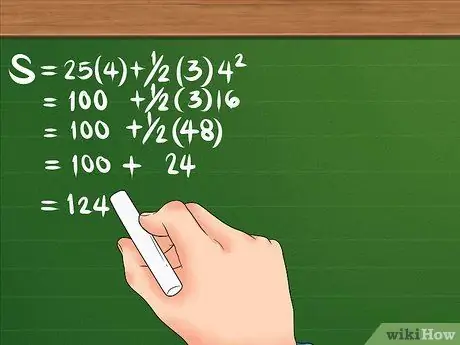
שלב 3. חשב את העקירה על ידי ביצוע סדר הפעולות הנכון
דרך מהירה לעזור לכם לזכור את רצף הפעולות היא גשר החמורים Kur ir Kua ci Kadang Ba wa Turtles. זה מייצג את הסדר הנכון: סוגריים, ריבועים, כפל, חלוקה, חיבור וחיסור.
הבה נבחן את הנוסחה שוב: S = 25 (4) + 1/2 (3) 4². ראשית, ריבוע 4, התוצאה היא 16. לאחר מכן, כפל 16 ב -3, ונעשה 48; לאחר מכן הכפל גם 25 ב- 4, כדי ליצור 100. מחלקים 48 ב- 2, כדי ליצור 24. המשוואה שלך צריכה להיראות כך: S = 100 + 24. ברגע שאתה מחבר את שניהם, התזוזה היא 124 מטר
חלק 4 מתוך 5: חישוב תזוזה זוויתית

שלב 1. מצא את התזוזה הזוויתית כשהאובייקט נע בנתיב מעגלי
למרות שתמיד תחשיב את העקירה באמצעות קו ישר, יהיה עליך למצוא את ההבדל בין מיקומי ההתחלה והסיום של האובייקט כשהוא נע בנתיב מעגלי.
- תארו לעצמכם ילדה יושבת על מסלול שמח. כשהוא מסתובב עם הקרוסלה, הוא ינוע בנתיב מעגלי. עקירה זוויתית מנסה למצוא את המרחק הקצר ביותר בין המיקום ההתחלתי והאחרון כשהאובייקט אינו נע בקו ישר.
- הנוסחה לעקירה זוויתית היא: = S/r, כאשר S היא התזוזה הלינארית, r הוא הרדיוס, והוא התזוזה הזוויתית. תזוזה לינארית היא כמה רחוק אובייקט נע לאורך קשת. הרדיוס הוא מרחק האובייקט למרכז המעגל. תזוזה זוויתית היא הערך שאנו רוצים למצוא.

שלב 2. חבר את התזוזה הליניארית והרדיוס למשוואה
זכור כי הרדיוס הוא המרחק ממרכז המעגל; כמה בעיות יגידו לך את קוטר העיגול, אותו יש לחלק ב- 2 כדי למצוא את הרדיוס.
- להלן בעיה לדוגמא: נערה רוכבת על סבבה. המושב נמצא מטר אחד ממרכז המעגל (הרדיוס). אם הילדה נעה במסלול קשת 1.5 מטר (תזוזה לינארית), מה היא התזוזה הזוויתית שלה?
- המשוואה שלך תיראה כך: = 1.5/1.
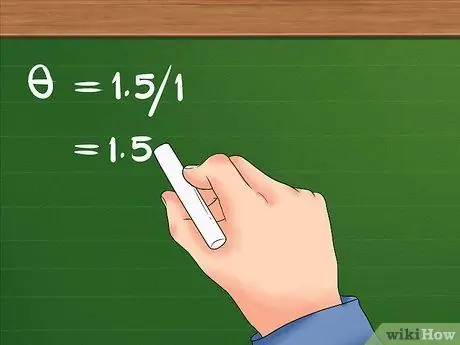
שלב 3. חלק את התזוזה הלינארית ברדיוס
חלוקה זו תגרום לתזוזה הזוויתית של האובייקט.
- לאחר חלוקה של 1.5 על 1, התוצאה היא 1.5. התזוזה הזוויתית של הילדה היא 1.5 רדיאנים.
- מכיוון שהתזוזה הזוויתית מודדת כמה מסתובב אובייקט ממיקומו ההתחלתי, יש למדוד אותו כזווית ולא כמרחק. ראדיאן היא היחידה המשמשת למדידת זוויות.
חלק 5 מתוך 5: הבנת הגירה
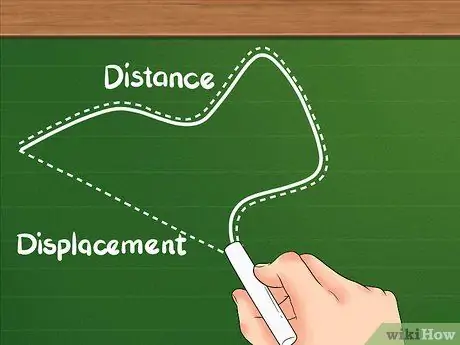
שלב 1. דעו כי למרחק יש הגדרה שונה מאשר תזוזה
המרחק מראה עד כמה המרחק הכולל שעבר החפץ.
- מרחק ידוע לרוב ככמות סקלרית. המרחק מציג את המרחק שעובר אובייקט ללא קשר לכיוון האובייקט.
- לדוגמה, אם אתה הולך 2 צעדים מזרחה, 2 צעדים דרומה, 2 צעדים מערבה ולאחר מכן 2 צעדים צפונה, תחזור למיקום ההתחלה שלך. למרות שעברת את הסכום מֶרְחָק 10 צעדים משם, אתה פשוט מהלך / לזוז / לעבור 0 צעדים משם מכיוון שהמיקום הסופי שלך זהה למיקום ההתחלה שלך (הנתיב שלך דומה לתיבה).

שלב 2. הבן שתזוזה היא ההבדל בין שני מיקומים
העקירה אינה סכום התנועה הכולל כמו מרחק; משמרות מתמקדות באזור שבין מיקומי ההתחלה והסיום שלך.
- העקירה נקראת כמות וקטורית ומציגה את השינוי במיקום האובייקט בהתחשב בכיוון התנועה של האובייקט.
- לדוגמה, אתה הולך מזרחה במשך 5 מדרגות. אם תחזור מערבה 5 מדרגות, תזוז בכיוון ההפוך מהמיקום המקורי שלך. למרות שעשית 10 שלבים, המיקום שלך לא השתנה; התזוזה שלך היא 0 שלבים.

שלב 3. זכור את המילים קדימה ואחורה כשאתה מנסה לדמיין עקירה
תנועה בכיוון ההפוך מבטלת את תזוזה של אובייקט.
דמיינו מאמן כדורגל הלוך ושוב בצד. בעודו צועק על השחקנים, הוא נע משמאל לימין מספר פעמים. אם אתה צופה בו כשהוא נע משמאל לימין, אתה מבחין במרחק הכולל שעבר. עם זאת, נניח שהמאמן עוצר לדבר עם הקוורטרבק בצד. אם הוא נמצא בנקודה שונה מהמיקום ההתחלתי שלו לפני המעבר, אז אתה צופה במעבר של המאמן

שלב 4. דע שהתזוזה נמדדת באמצעות נתיב ישר, ולא נתיב מעגלי
כדי למצוא עקירה, עליך למצוא את הדרך הקצרה והיעילה ביותר לחישוב ההפרש בין שתי נקודות.
- נתיב מעגלי יוביל אותך ממיקום ההתחלה שלך למיקום הסופי שלך, אך הוא אינו הנתיב הקצר ביותר. כדי לעזור לך לדמיין את זה, דמיין שאתה הולך בקו ישר ואתה נתקל בעמוד. אתה לא יכול לפרוץ את העמוד הזה, אז אתה עוקף אותו. למרות שהעמדה הסופית שלך זהה כאילו פרצת את העמוד, תצטרך צעדים נוספים כדי להגיע ליעד זה.
- למרות שהתזוזה מייצגת נתיב ישר, דע כי אתה יכול למדוד את העקירה של אובייקט שהוא כַּיוֹם לנוע בנתיב מעגלי. עקירה זו נקראת תזוזה זוויתית וניתן לחשב אותה על ידי מציאת הנתיב הקצר ביותר מהמיקום ההתחלתי למיקום הסופי.

שלב 5. דע שהתזוזה יכולה להיות שלילית, בניגוד למרחק
אם מגיעים למיקום הסופי שלך על ידי תנועה בכיוון ההפוך לכיוון ההתחלתי, אז התזוזה שלך שלילית.
- לדוגמה, אנו צועדים 5 מדרגות מזרחה ולאחר מכן 3 מדרגות מערבה. למרות שבחישוב אתה עובר 2 צעדים ממיקום ההתחלה שלך, התזוזה שלך היא -2 מכיוון שאתה נע בכיוון ההפוך. המרחק שלך תמיד יהיה חיובי מכיוון שאתה לא יכול לספור אחורה בצעדים, קילומטרים וכו '.
- תזוזה שלילית לא אומרת שהתזוזה פוחתת. שלילי רק אומר שהכיוון הפוך.

שלב 6. הבינו שלפעמים המרחק והתזוזה יכולים להיות זהים
אם אתה הולך ישר 25 מדרגות ועוצר, המרחק שאתה נוסע יהיה שווה לתזוזה מהמיקום המקורי שלך.
- זה חל רק כאשר אתה עובר ממקום אחד ממקום ההתחלה שלך בקו ישר. לדוגמה, אתה גר בסן פרנסיסקו, קליפורניה, ומקבל עבודה חדשה בלאס וגאס, נבדה. אתה צריך לעבור ללאס וגאס כדי להיות קרוב לעבודה שלך. אם אתה עולה על מטוס שעף יָשָׁר מסן פרנסיסקו ללאס וגאס, תטייל באותו מרחק ותזוזה x.
- עם זאת, אם תסעו מסן פרנסיסקו ללאס וגאס, תסעו למרחק x, אך תסעו מרחק y. מכיוון שלנהיגה במכונית בדרך כלל יש כיוונים משתנים (מזרחית לכביש זה, ממערב לכביש זה), אתה נוסע למרחקים ארוכים יותר מהמרחק הקצר ביותר בין שתי הערים.






