- מְחַבֵּר Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:15.
- שונה לאחרונה 2025-01-23 12:18.
ערך ה- P הוא מדידה סטטיסטית המסייעת למדענים לקבוע אם השערתם נכונה. ערך P משמש כדי לקבוע אם תוצאות הניסוי שלהם נמצאות בטווח הערכים הנורמליים לדברים שנחקרו. בדרך כלל, אם ערך ה- P של מערך נתונים יורד מתחת לערך מסוים שנקבע מראש (למשל, 0.05), המדענים ידחו את השערת האפס של הניסוי שלהם - במילים אחרות, הם יפסלו השערה שבה יש למשתנה הניסוי ללא השפעה משמעותית על התוצאה. כיום, ערכי p נמצאים בדרך כלל בטבלאות הפניה על ידי חישוב ערך הצ'י בריבוע.
שלב

שלב 1. קבע את התוצאות הצפויות של הניסוי שלך
בדרך כלל, כאשר מדענים עורכים ניסוי ובוחנים את התוצאות, יש להם כבר מושג לגבי התוצאות הרגילות או הרגילות מראש. זה יכול להתבסס על תוצאות ניסויים קודמים, מערכי נתונים תצפיתיים אמינים, ספרות מדעית ו/או מקורות אחרים. לצורך הניסוי, קבע את התוצאה הצפויה שלך ורשום אותה כמספר.
דוגמה: נניח שמחקר קודם הראה כי ברמה הארצית הונפקו כרטיסים במהירות מופרזת יותר למכוניות אדומות מאשר למכוניות כחולות. נניח שהתוצאה הממוצעת ברמה הלאומית מראה יחס של 2: 1 כאשר היחס בין מכוניות אדומות הוא יותר. אנחנו רוצים לברר אם גם המשטרה בעיר שלנו מקבלת את אותה נטייה על ידי ניתוח הכרטיס המהיר שהוציאה המשטרה בעיר שלנו. אם היינו לוקחים מדגם אקראי של 150 כרטיסי מהירות שניתן למכוניות אדומות וכחולות בעיר שלנו, היינו מצפים 100 לרכב אדום ו 50 למכוניות כחולות אם יחידת המשטרה בעירנו נותנת כרטיס לפי ההשוואה ברמה הלאומית.

שלב 2. קבע את התצפיות הניסיוניות שלך
כעת לאחר שקבעת את הערך הצפוי שלך, תוכל להריץ את הניסוי ולמצוא את הערך האמיתי (או התצפית). שוב, רשום את התוצאה כמספר. אם נתפעל כמה תנאי ניסוי והתוצאות הנצפות שונות מהתוצאות הצפויות, קיימות שתי אפשרויות: או שזה קרה במקרה, או שמניפולציה של המשתנים הניסיוניים היא שגרמה להבדל הזה. מטרת מציאת ערך p היא בעצם לקבוע אם התוצאות הנצפות שונות מהתוצאות הצפויות עד לנקודה שבה לא ניתן לדחות את השערת האפס-ההשערה שאין קשר בין המשתנה הניסיוני לתוצאות הנצפות.
דוגמה: נניח שבעיר שלנו אנו בוחרים באקראי 150 כרטיסי מהירות המוקנים למכוניות אדומות וכחולות כאחד. אנחנו מקבלים 90 כרטיס לרכב אדום ו 60 לרכב הכחול. זה שונה מהתוצאה שציפינו כלומר 100 ו 50. האם המניפולציה הניסיונית שלנו (במקרה זה, שינוי מקור הנתונים מארצי למקומי) גרמה לשינוי כלשהו בתוצאות, או שמא למשטרת העיר שלנו היו נטיות זהות לרמה הלאומית, ורק עכשיו צפינו צירוף מקרים? ערך p יעזור לנו לקבוע אותו.

שלב 3. קבע את דרגות החופש לניסוי שלך
דרגות החופש הן מדד לכמות השונות במחקר, הנקבעת על פי מספר הקטגוריות שאתה בוחן. המשוואה למידות החופש היא דרגות חופש = n-1, כאשר n הוא מספר הקטגוריות או המשתנים שניתחו בניסוי שלך.
-
דוגמה: לניסוי שלנו שתי קטגוריות של תוצאות: אחת למכונית האדומה ואחת למכונית הכחולה. כך, בניסוי שלנו, יש לנו 2-1 = דרגת חופש אחת.
אם נשווה מכוניות אדומות, כחולות וירוק, יהיה לנו
שלב 2. דרגות חופש וכן הלאה.

שלב 4. השווה את התוצאות הצפויות לתוצאות שנצפו באמצעות צ'י בריבוע
צ'י בריבוע (כתוב x2) הוא ערך מספרי המודד את ההבדל בין הערכים הצפויים והצפויים מהניסוי. המשוואה לצ'י בריבוע היא: איקס2 = ((o-e)2/e), כאשר o הוא הערך הנצפה ו- e הוא הערך הצפוי. הוסף את תוצאות משוואה זו לכל התוצאות האפשריות (ראה להלן).
- שים לב שמשוואה זו משתמשת באופרטור (סיגמא). במילים אחרות, עליך לחשב ((| o-e | -.05)2/ה) עבור כל תוצאה אפשרית, ולאחר מכן צרו את התוצאות כדי לקבל את הערך בריבוע הצ'י. בדוגמה שלנו, יש לנו שתי תוצאות - מכונית שמקבלת כרטיס אדום או כחול. לפיכך, אנו יכולים לחשב ((o-e)2/ה) פעמיים - פעם לרכב האדום ופעם לרכב הכחול.
-
דוגמה: בואו נחבר את הערכים והתצפיות הצפויות שלנו למשוואה x2 = ((o-e)2/e). זכור שבגלל אופרטור הסיגמא, עלינו לחשב ((o-e)2/ה) פעמיים - פעם לרכב האדום ופעם לרכב הכחול. שלבי העיבוד הם כדלקמן:
- איקס2 = ((90-100)2/100) + (60-50)2/50)
- איקס2 = ((-10)2/100) + (10)2/50)
- איקס2 = (100/100) + (100/50) = 1 + 2 = 3.

שלב 5. בחר רמת משמעות
כעת, כאשר אנו יודעים את דרגות החופש של ערכת הניסוי שלנו ואת ערך הצ'י בריבוע, יש רק דבר אחרון שעלינו לעשות לפני שנוכל למצוא את ערך ה- p שלנו-עלינו לקבוע את רמת המשמעות. ביסודו של דבר, רמת המובהקות היא מדידה של עד כמה אנו בטוחים בתוצאות שלנו - רמת משמעות נמוכה תואמת את ההסתברות הנמוכה שתוצאת הניסוי נובעת ממקרה ולהיפך. רמת המשמעות כתובה כעשרונית (למשל 0.01), המתאימה לאחוז הסיכוי שתוצאת הניסוי נובעת מסיכוי (במקרה זה, 1%).
- על פי מוסכמה, מדענים בדרך כלל קובעים ערך מובהק לניסויים שלהם על 0.05 או 5 אחוזים. המשמעות היא שלתוצאות ניסיוניות המתאימות לרמה זו של משמעות יש לכל היותר סיכוי של 5% לצירוף מקרים. במילים אחרות, יש סיכוי של 95% שהתוצאות נובעות ממניפולציה של המדען עם המשתנים הניסיוניים, ולא מקריות. עבור רוב הניסויים, ביטחון של 95% לגבי הקשר בין שני המשתנים נחשב להצלחת הוכחת הקשר בין השניים.
- דוגמה: לדוגמא המכונית האדומה והכחולה שלנו, בואו נעקוב אחר ההסכם המדעי ונקבע את רמת המשמעות שלנו 0, 05.
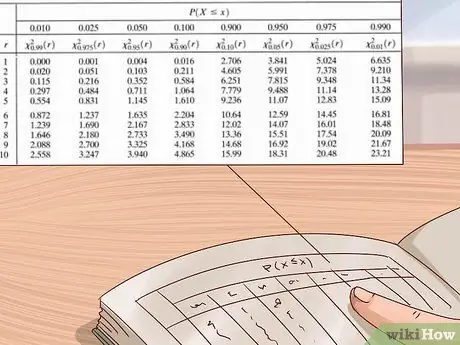
שלב 6. השתמש בטבלת החלוקה של צ'י מרובע כדי להעריך את ערך ה- p שלך
מדענים וסטטיסטיקאים משתמשים בטבלאות ערכים גדולות לחישוב ערכי p לניסויים שלהם. טבלה זו נכתבת בדרך כלל כאשר הציר האנכי משמאל מציג את דרגות החופש והציר האופקי בחלק העליון מציג את ערכי p. השתמש בטבלה זו על ידי מציאת תחילת דרגות החופש שלך, ולאחר מכן קריאת השורות משמאל לימין עד שתמצא את הערך הראשון הגדול מערך הצ'י בריבוע שלך. תסתכל על ערך p בראש העמודה-ערך p שלך נמצא בין ערך זה לערך הבא בגודלו (הערך הנכון משמאל לו).
- טבלאות חלוקה של כיכר צ'י זמינות ממגוון מקורות - ניתן למצוא אותן בקלות באינטרנט או בספרי לימוד מדעיים או סטטיסטיים. אם אין לך כזה, השתמש בטבלה המוצגת בתמונה למעלה או בטבלה מקוונת בחינם, כמו זו שמספקת medcalc.org כאן.
-
דוגמה: הצ'י בריבוע שלנו הוא 3. אז בואו נשתמש בטבלת חלוקת הצ'י בריבוע בתמונה למעלה כדי למצוא ערך p משוער. מכיוון שאנו יודעים שלניסוי שלנו יש רק
שלב 1. דרגות חופש, נתחיל מהטבלה העליונה. אנו עוברים משמאל לימין בשורה זו עד שנמצא ערך גבוה מ-
שלב 3. - ערך הצ'י בריבוע שלנו. הערך הראשון שאנו מוצאים הוא 3.84. במבט בעמודה זו, אנו רואים שערך p המקביל הוא 0.05. המשמעות היא שערך p שלנו הוא בין 0.05 ל 0.1 (ערך ה- p הבא בגודלו בטבלה).

שלב 7. החליט אם לדחות או להגן על השערת האפס שלך
מכיוון שמצאת ערך p משוער לניסוי שלך, אתה יכול להחליט אם לדחות או לא לדחות את השערת האפס של הניסוי (כזכור, זוהי ההשערה שלמשתנה הניסוי שאתה מניפולציה לא השפיעה על התוצאות שראית). אם ערך p שלך נמוך מערך המשמעות שלך, מזל טוב-הוכחת שיש סבירות גבוהה שיש קשר בין המשתנים שאתה מניפולציה לבין התצפיות שלך. אם ערך ה- p שלך גדול מערך המשמעות שלך, אינך יכול לומר בוודאות שהתוצאות שאתה צופה בהן הן תוצאה של צירוף מקרים או מניפולציה של הניסוי שלך.
- דוגמה: ערך ה- p שלנו הוא בין 0.05 ל -0.1. כלומר, הוא לא פחות מ- 0.05, כך שלצערנו, אנו לא יכול לדחות את השערת האפס שלנו. המשמעות היא שאיננו מגיעים לגבול האמון המינימלי של 95% שקבענו, כך שניתן לומר כי המשטרה בעירנו נותנת כרטיסי כרטוס למכוניות אדומות וכחולות ביחס השונה למדי מהממוצע הארצי.
- במילים אחרות, יש סיכוי של 5-10% שהתצפיות שלנו אינן תוצאה של שינוי מיקום (ניתוח העיר שלנו, ולא החלק כולו), אלא צירופי מקרים. מכיוון שאנו מחפשים הסתברות של פחות מ -5%, איננו יכולים לומר שכן מְשׁוּכנָע שהמשטרה בעירנו נוטה לרכוש מכוניות אדומות - יש אפשרות קלה אך סטטיסטית מאוד שונה שאין לה נטייה זו.
טיפים
- מחשבון מדעי יקל על החישובים הרבה יותר. אתה יכול גם לחפש מחשבונים באינטרנט.
- ניתן לחשב ערכי p באמצעות מספר תוכנות מחשב, כולל תוכנות גיליון אלקטרוני נפוצות ותוכנות סטטיסטיות מיוחדות יותר.






